หากพูดถึงเนื้อหาการเรียน ม.4 หรือการติวคณิตศาสตร์ ม.4 คงหนีไม่พ้น บทตรรกศาสตร์ ที่น้อง ๆ จะได้เรียนกันตั้งแต่ช่วง ม.4 เทอม 1 ซึ่งบทนี้มีความสำคัญอย่างมาก เป็นบทที่ว่าด้วยความเป็นเหตุเป็นผล จึงเป็นพื้นฐานสำคัญในการสรุปความ และการให้เหตุผลอย่างถูกต้องมีหลักการ และเป็นบทสำคัญที่ออกสอบในข้อสอบคณิคศาสตร์แทบจะทุกสนาม วันนี้ พี่กอล์ฟ – อ.ชวลิต กุลกีรติการ จะพามารู้จักและทำความเข้าใจกับบทตรรกศาสตร์ให้มากขึ้น ไปดูกันเลย!!
ตรรกศาสตร์ คืออะไร
ตรรกศาสตร์ เป็นศาสตร์ที่ศึกษาเกี่ยวกับเหตุและผล เป็นพื้นฐานสำคัญในการพิสูจน์ทฤษฎีบททางคณิตศาสตร์ต่าง ๆ และสามารถนำไปใช้ต่อยอดในด้านอื่น ๆ เช่น คอมพิวเตอร์ เป็นต้น
ประพจน์ คืออะไร
ประพจน์ (Statement) คือ ประโยคหรือข้อความที่เป็นจริงหรือเท็จอย่างใดอย่างหนึ่งเท่านั้น ซึ่งจะอยู่ในรูปบอกเล่าหรือปฏิเสธก็ได้ นิยมใช้อักษรภาษาอังกฤษตัวพิมพ์เล็ก เช่น p , q , r แทนประพจน์
โดยเราจะเรียกการเป็น “จริง” หรือ “เท็จ” ของแต่ละประพจน์ว่า ค่าความจริง (Truth Value) และจะใช้ T แทนค่าความจริงที่ เป็นจริง (True) และ F แทนค่าความจริงที่ เป็นเท็จ (False)
ตัวอย่างประโยคที่เป็นประพจน์
- เดือนมกราคม มี 31 วัน
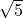เป็นจำนวนเต็มบวก
ประโยคที่ไม่เป็นประพจน์ คือ ประโยคที่ไม่สามารถระบุได้ว่าเป็นจริงหรือเท็จ เช่น ประโยคคำถาม, คำสั่ง, ขอร้อง, อุทาน
ตัวเชื่อมประพจน์
ในบทตรรกศาสตร์นี้ เราจะมีการนำประพจน์มากกว่า 1 ประพจน์มาเชื่อมกัน เกิดเป็นประพจน์ใหม่ โดยใช้ ตัวเชื่อม (Connective) ต่าง ๆ ดังนี้
- “และ” ใช้สัญลักษณ์ ∧
- “หรือ” ใช้สัญลักษณ์ ∨
- “ถ้า…แล้ว…” ใช้สัญลักษณ์ →
- “ก็ต่อเมื่อ” ใช้สัญลักษณ์ ↔
- “นิเสธ” ใช้สัญลักษณ์ ~
ตารางค่าความจริงของประพจน์
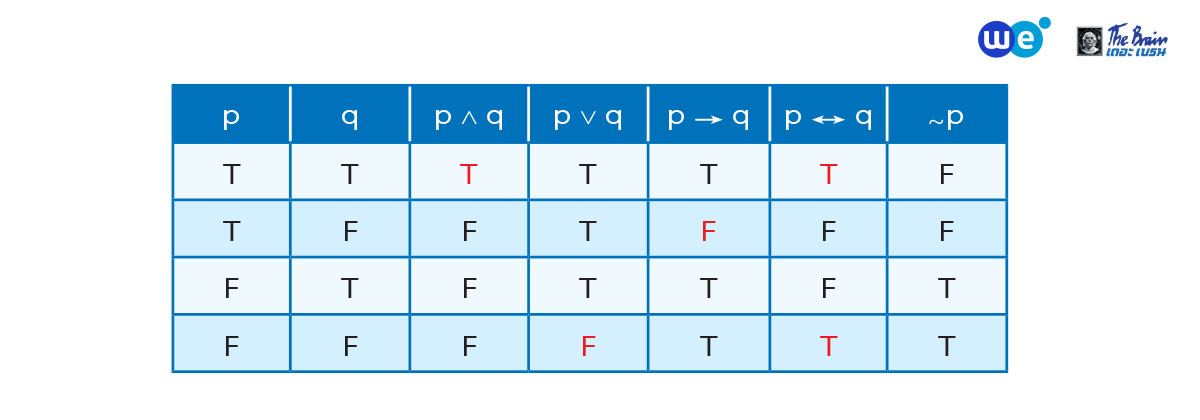
จากตารางการแจกแจงค่าความเป็นจริงของประพจน์ น้อง ๆ สามารถสรุปได้ดังนี้
- “และ” (∧) จะเป็นจริงเพียงกรณีเดียว คือ T ∧ T เป็น T
- “หรือ” (∨) จะเป็นเท็จเพียงกรณีเดียว คือ F ∨ F เป็น F
- “ถ้า…แล้ว…” (→) จะเป็นเท็จเพียงกรณีเดียว คือ T → F เป็น F
- “ก็ต่อเมื่อ” (↔) ถ้ามีค่าความจริงเหมือนกันจะเป็นจริง ไม่เหมือนกันจะเป็นเท็จ
- “นิเสธ” (~) จะมีค่าความจริงตรงข้ามกับประพจน์เดิม
ข้อมูลจากตารางค่าความเป็นจริงของประพจน์ดังกล่าวนั้นทำให้น้อง ๆ ได้รู้เพิ่มเติมว่า
- p ∧ q จะมีค่าความจริงเป็นจริง เมื่อ p และ q มีค่าความจริงเป็นจริงทั้งสองประพจน์
p ∧ q จะมีค่าความจริงเป็นเท็จ เมื่อ p หรือ q มีค่าความจริงเป็นเท็จ อย่างน้อยหนึ่งประพจน์ - p ∨ q จะมีค่าความจริงเป็นเท็จ เมื่อ p และ q มีค่าความจริงเป็นเท็จทั้งสองประพจน์
p ∨ q จะมีค่าความจริงเป็นจริง เมื่อ p หรือ q มีค่าความจริงเป็นจริง อย่างน้อยหนึ่งประพจน์ - p → q จะมีค่าความจริงเป็นเท็จ เมื่อ p มีค่าความจริงเป็นจริง และ q มีค่าความจริงเป็นเท็จ
ถ้า p มีค่าความจริงเป็นเท็จ แล้ว p → q จะมีค่าความจริงเป็นจริงโดยไม่จำเป็นต้องรู้ ค่าความจริงของ q
ถ้า q มีค่าความจริงเป็นจริง แล้ว p → q จะมีค่าความจริงเป็นจริงโดยไม่จำเป็นต้องรู้ ค่าความจริงของ p - p ↔ q จะมีค่าความจริงเป็นจริง เมื่อ p และ q มีค่าความจริงเหมือนกัน
p ↔ q จะมีค่าความจริงเป็นเท็จ เมื่อ p และ q มีค่าความจริงต่างกัน
รูปแบบของประพจน์ที่สมมูลกัน
ในทางตรรกศาสตร์ ถ้ารูปแบบของประพจน์ 2 รูปแบบใดมีค่าความจริงตรงกันกรณีต่อกรณี แล้ว สามารถนำไปใช้แทนกันได้ จะเรียกรูปแบบของประพจน์ทั้ง 2 ว่า “รูปแบบของประพจน์ที่สมมูลกัน” และใช้สัญลักษณ์ ≡ แทนการสมมูลกัน
รูปแบบของประพจน์สำคัญที่สมมูลกันที่น้อง ๆ ควรรู้จัก
- p ∧ q ≡ q ∧ p
- p ∨ q ≡ q ∨ p
- (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
- (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
- p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
- p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
- p → q ≡ ~p ∨ q
- p → q ≡ ~q → ~p
- p ↔ q ≡ (p → q) ∧ (q → p)
- ~(~p) ≡ p
- ~(p ∧ q) ≡ ~p ∨ ~q
- ~(p ∨ q) ≡ ~p ∧ ~q
- ~(p → q) ≡ p ∧ ~q
- ~(p ↔ q) ≡ ~p ↔ q ≡ p ↔ ~q
สัจนิรันดร์
รูปแบบของประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี เรียกว่า “สัจนิรันดร์” หัวข้อสัจนิรันดร์เป็นเรื่องที่ออกข้อสอบบ่อยมาก ๆ โดยแนวข้อสอบส่วนมากจะกำหนดประพจน์มาให้ และให้เราตรวจสอบว่าประพจน์ที่กำหนดมาให้นั้นเป็นสัจนิรันดร์หรือไม่ ซึ่งวิธีการตรวจสอบทำได้ 2 วิธี คือ
1. วิธีการสร้างตารางค่าความจริง
ถ้า ค่าความจริงของประพจน์นั้นเป็นจริงทุกกรณี (ทุกบรรทัดในตาราง) จะสรุปได้ว่าประพจน์นั้นเป็นสัจนิรันดร์ แต่ถ้ามีบางกรณีในตารางมีค่าความจริงเป็นเท็จ ประพจน์นั้นจะไม่เป็นสัจนิรันดร์
2. วิธีการหาข้อขัดแย้ง
วิธีนี้ทำโดยสมมุติให้รูปแบบของประพจน์ที่ต้องการตรวจสอบเป็น “เท็จ” แล้วจึงหาค่าความจริงของประพจน์ย่อย จากนั้นดูว่ามีข้อขัดแย้งเกิดขึ้นหรือไม่ ถ้า มีข้อขัดแย้ง แสดงว่า รูปแบบของประพจน์นั้นเป็นสัจนิรันดร์ แต่ถ้าไม่มีข้อขัดแย้ง แสดงว่ารูปแบบของประพจน์นั้นไม่เป็นสัจนิรันดร์
การอ้างเหตุผล
การอ้างเหตุผล คือ การอ้างว่า เมื่อมีประพจน์ p1, p2, … , pn ชุดหนึ่ง แล้วสามารถสรุปประพจน์ C ประพจน์หนึ่งได้ การอ้างเหตุผลประกอบด้วยส่วนสำคัญ 2 ส่วน คือ
- เหตุ หรือ สิ่งที่กำหนดให้ ได้แก่ ประพจน์ p1, p2, … , pn
- ผล หรือ ข้อสรุป คือ ประพจน์ C
เหตุ 
ผล 
สำหรับ วิธีการตรวจสอบว่าการอ้างเหตุผลที่กำหนดให้สมเหตุสมผลหรือไม่ ทำได้โดยนำเหตุทุกประพจน์มาเชื่อมกันด้วยตัวเชื่อม “และ” จากนั้นนำไปเชื่อมกับผลด้วยตัวเชื่อม “ถ้า… แล้ว…” จะได้
นำประพจน์ที่ได้นี้ไปตรวจสอบสัจนิรันดร์ ถ้าเป็นสัจนิรันดร์ การอ้างเหตุผลนี้สมเหตุสมผล (Valid) แต่ถ้าไม่เป็นสัจนิรันดร์ การอ้างเหตุผลนี้ไม่สมเหตุสมผล (Invalid)
ประโยคเปิดและตัวบ่งปริมาณ
ประโยคเปิด (Open Sentence) คือ ประโยคบอกเล่าหรือประโยคปฏิเสธที่มีตัวแปร จึงไม่สามารถบอกได้ว่ามีค่าความจริงเป็นจริงหรือเท็จ แต่เมื่อแทนตัวแปรในประโยคเปิดด้วยสมาชิกในเอกภพสัมพัทธ์ จะได้ประพจน์ที่สามารถบอกได้ว่าค่าความจริงเป็นจริงหรือเท็จ ใช้สัญลักษณ์ P(x) แทนประโยคเปิดที่มีตัวแปร x
ตัวบ่งปริมาณ (Quantifier)
- สำหรับ … ทุกตัว แทนด้วยสัญลักษณ์ ∀
- สำหรับ … บางตัว แทนด้วยสัญลักษณ์ ∃
เราสามารถ หาค่าความจริงของประโยคที่มีตัวบ่งปริมาณ ได้ดังนี้
- ∀ x [P(x)] มีค่าความจริงเป็นจริง ก็ต่อเมื่อแทนตัวแปร x ใน P(x) ด้วยสมาชิกแต่ละตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นจริงทั้งหมด
- ∀ x [P(x)] มีค่าความจริงเป็นเท็จ ก็ต่อเมื่อแทนตัวแปร x ใน P(x) ด้วยสมาชิกอย่างน้อย 1 ตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นเท็จ
- ∃ x [P(x)] มีค่าความจริงเป็นจริง ก็ต่อเมื่อแทนตัวแปร x ใน P(x) ด้วยสมาชิกอย่างน้อย 1 ตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นจริง
- ∃ x [P(x)] มีค่าความจริงเป็นเท็จ ก็ต่อเมื่อแทนตัวแปร x ใน P(x) ด้วยสมาชิกแต่ละตัวในเอกภพสัมพัทธ์ แล้วได้ประพจน์ที่มีค่าความจริงเป็นเท็จทั้งหมด
ฝึกทำโจทย์ตรรกศาสตร์ พร้อมเฉลย - พี่กอล์ฟ เดอะเบรน
โจทย์ตรรกศาสตร์ ข้อที่ 1
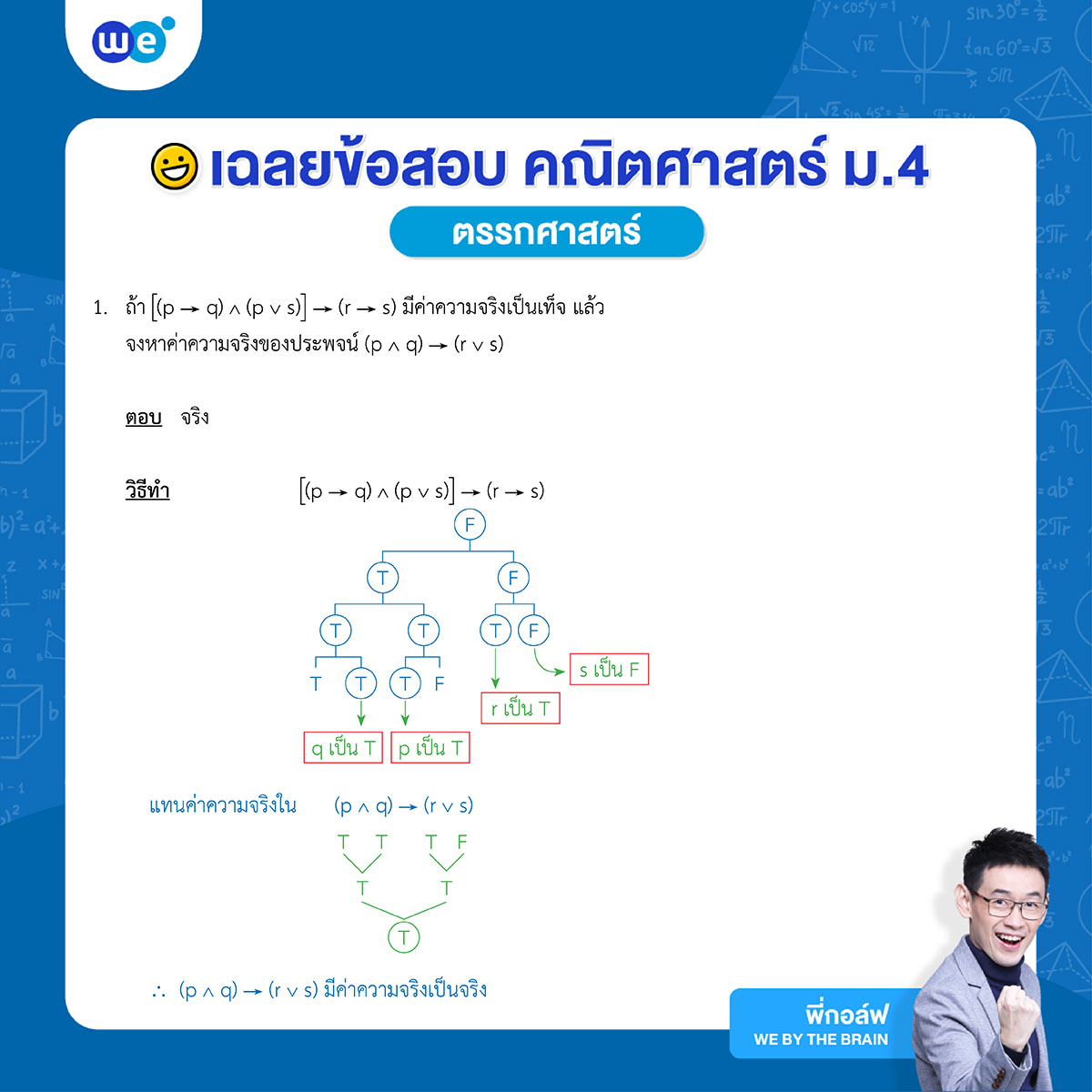
โจทย์ตรรกศาสตร์ ข้อที่ 2
โจทย์ตรรกศาสตร์ ข้อที่ 3
สรุปเรื่องเนื้อหาตรรกศาสตร์ ม.4
และนี่คือตัวอย่างเนื้อหาส่วนหนึ่งของตรรกศาสตร์ ม.4 ที่ออกข้อสอบอยู่บ่อย ๆ ในระดับ ม.ปลาย หากน้อง ๆ ทำความเข้าใจเนื้อหาของบทเรียน ตรรกศาสตร์ รู้ความหมายของประพจน์ สัจนิรันดร์ การอ้างเหตุผล ประโยคเปิดและตัวบ่งปริมาณ และจับจุดสำคัญของบทนี้ได้ น้อง ๆ ก็สามารถนำความรู้ไปทำข้อสอบและประยุกต์ใช้ได้กับบทเรียนต่าง ๆ ได้ง่ายขึ้นเยอะเลยครับ
ติวคณิตศาสตร์ ม.4 กับ WE BY THE BRAIN พร้อมพิชิตเกรด 4 และสนามสอบเข้ามหาวิทยาลัย
หากน้อง ๆ ม.ปลาย ต้องการติวคณิตศาสตร์ ม.ปลาย ให้แม่นขึ้น เพื่อให้ทำข้อสอบได้ง่ายขึ้นหรืออยากคว้าเกรด 4 สามารถสมัคร คอร์สคณิตศาสตร์ ม.4 เทอม 1 รวมทุกบท กับ WE BY THE BRAIN ได้เลย
สมัครคอร์สนี้ดียังไง?
✔ เนื้อหาในคอร์สเรียนตรงตามหลักสูตรของ สสวท. ประกอบด้วยเซต ตรรกศาสตร์ และระบบจำนวนจริง
✔ สอนโดยพี่ ๆ ติวเตอร์ทีมคณิตศาสตร์ที่มีประสบการณ์การสอนกว่า 18 ปี ที่จะช่วยปูพื้นฐานให้น้อง ๆ อย่างละเอียด
✔ พร้อมพาฝึกทำโจทย์อย่างเข้มข้น ไล่ระดับตั้งแต่ง่ายไปจนถึงยาก ที่เป็นข้อสอบแข่งขันจากสนามสอบทั้งในและต่างประเทศ
✔ เสริมด้วยเทคนิคทริกลัดแก้โจทย์ไว ที่จะช่วยให้น้อง ๆ สามารถทำข้อสอบปรนัยได้อย่างรวดเร็วยิ่งขึ้น
คอร์สนี้เหมาะกับใคร?
✔ เหมาะสำหรับน้อง ม.3 ที่กำลังจะขึ้น ม.4 และต้องการเตรียมตัวล่วงหน้า
✔ เหมาะสำหรับน้อง ม.4 ที่ต้องการเรียนควบคู่ไปกับที่โรงเรียน เพื่อคว้าเกรด 4 วิชาคณิตศาสตร์ และเป็นพื้นฐานสำคัญในการเตรียมตัวสอบเข้ามหาวิทยาลัย วิชาคณิตศาสตร์ประยุกต์1 A-Level ในระบบ TCAS
ใครอยากเก่งคณิต อยากได้โจทย์และเทคนิคดี ๆ จาก พี่ ๆ ติวเตอร์ ทีมคณิตศาสตร์ รีบกดติดตามก่อนใครได้ที่ช่องทางด้านล่างนี้เลย!
- Facebook Page : WE BY THE BRAIN
- Instagram : webythebrain
- Youtube : WE BY THE BRAIN
- Tiktok : คณิต เดอะเบรน
- Lemon8 : คณิต เดอะเบรน
อ.ชวลิต กุลกีรติการ (พี่กอล์ฟ)
วิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย เกียรตินิยม ประสบการณ์การสอน 24 ปี
