สำหรับน้อง ๆ คนไหนที่กำลังเรียนเกี่ยวกับการแก้อสมการเชิงเส้นตัวแปรเดียวนี้อยู่แล้วยังไม่ค่อยเข้าใจ หรือพยายามทำความเข้าใจแล้วแต่ยังสับสน จับต้นชนปลายไม่ถูก ขอให้น้อง ๆ อย่าเพิ่งถอดใจไป เพราะในบทความนี้ พี่ภูมิ – อ.สิทธิเดช เลนุกูล จะมาแนะวิธีการแก้อสมการเชิงเส้นตัวแปรเดียวแบบเข้าใจง่ายในบทความเดียว ที่มาพร้อมโจทย์และเฉลย
อสมการ คืออะไร
อสมการ (Inequality) คือ ประโยคสัญลักษณ์ที่แสดงถึงการไม่เท่ากันของจำนวน ซึ่งสามารถเป็นไปได้ทั้ง ไม่เท่ากับ (≠), มากกว่า (>), น้อยกว่า (<) , มากกว่าหรือเท่ากับ (≥) และน้อยกว่าหรือเท่ากับ (≤)
โดยความหมายของแต่ละสัญลักษณ์ คือ
- a ≠ b มีความหมายว่า a มีค่าไม่เท่ากับ b
- a < b มีความหมายว่า a มีค่าน้อยกว่า b (ไม่ถึง b)
- a > b มีความหมายว่า a มีค่ามากกว่า b (เกิน b)
- a ≤ b มีความหมายว่า a มีค่าน้อยกว่าหรือเท่ากับ b (ไม่เกิน b)
- a ≥ b มีความหมายว่า a มีค่ามากกว่าหรือเท่ากับ b (ไม่น้อยกว่า b)
อสมการเชิงเส้นตัวแปรเดียว
อสมการเชิงเส้นตัวแปรเดียว คือ ประโยคสัญลักษณ์ที่แสดงถึงความสัมพันธ์ของการไม่เท่ากัน และมีตัวแปรเพียงตัวเดียว โดยที่ตัวแปรนั้นมีเลขชี้กำลังเป็น 1 ซึ่งอสมการอาจมีคำตอบหรือไม่มีคำตอบก็ได้
คําตอบของอสมการเชิงเสนตัวแปรเดียว
คําตอบของอสมการ คือ จํานวนที่นําไปแทนค่าตัวแปรในอสมการ แล้วทําให้ได้อสมการที่เป็นจริงหรือสอดคล้องกับอสมการ และสำหรับจำนวนใดที่แทนค่าตัวแปรแล้วทำให้เกิดอสมการที่ไม่เป็นจริง แสดงว่าจำนวนนั้นไม่เป็นคำตอบของอสมการ
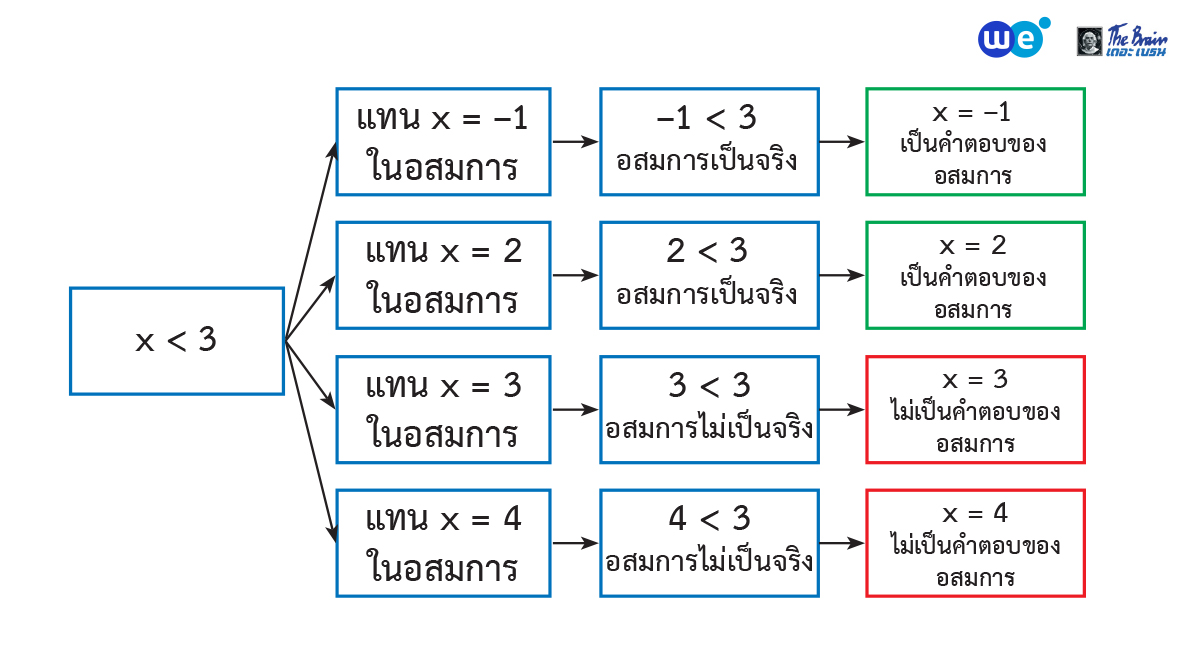
น้อง ๆ จะเห็นว่าคำตอบของอสมการไม่จำเป็นต้องมีเพียงแค่ค่าเดียวเท่านั้น โดยอสมการจะมีคำตอบได้ 3 ลักษณะ คือ
- มีจำนวนจริงทุกจำนวนเป็นคำตอบ
- มีจำนวนจริงบางจำนวนเป็นคำตอบ
- ไม่มีจำนวนจริงใดเป็นคำตอบ
ตัวอย่างของการหาคำตอบอสมการเชิงเส้นตัวแปรเดียว
ตัวอย่าง 1
จงหาคำตอบของอสมการ 2x – 2 > x + 5
วิธีทำ
จากโจทย์ +2 ทั้ง 2 ฝั่งจะได้ 2x – 2 + 2 > x + 5 + 2
ต่อมา -x ทั้ง 2 ฝั่งจะได้ 2x – x > x + 7 – x
พบว่า x > 7
ดังนั้น คำตอบของอสมการคือ จำนวนจริง x ทุกจำนวนที่มีค่ามากกว่า 7 นั่นเอง
ตัวอย่าง 2
จงหาคำตอบของอสมการ x+1 ≤ x+2
วิธีทำ
เนื่องจาก เมื่อแทน x ด้วยจำนวนจริงใด ๆ ใน x+1 ≤ x+2 แล้วจะได้อสมการที่เป็นจริงเสมอ
ดังนั้น คำตอบของอสมการ x+1 ≤ x+2 คือ จำนวนจริงทุกจำนวน
ตัวอย่าง 3
กำหนดให้ x เป็นจำนวนนับ
จงหาค่า x ที่สอดคล้องกับอสมการ 0 < x ≤ 1
วิธีทำ
จากโจทย์เมื่อแทน x = 1 จะได้ว่า 0 < 1 ≤ 1 อสมการเป็นจริง
แต่เมื่อแทน x = 2 จะได้ว่า 0 < 2 ≤ 1 อสมการไม่เป็นจริง
และสำหรับจำนวนนับ x ใดๆ ที่มากกว่า 2 เมื่อแทนลงในอสมการแล้วจะไม่เป็นจริงเสมอ
ดังนั้น อสมการจะมีเพียงคำตอบเดียวคือ x = 1 เป็นคำตอบของอสมการ
ตัวอย่าง 4
จงหาคำตอบของอสมการ x < x – 2
วิธีทำ
จากโจทย์ -x ทั้ง 2 ฝั่งจะได้ x – x < X -2 – x
พบว่า 0 < -2
ซึ่งอสมการไม่เป็นจริง (อาจารย์บางท่านอาจใช้คำว่า “อสมการเป็นเท็จ”)
หมายความว่าไม่มีจำนวนจริงใดที่แทนค่าใน x แล้วทำให้อสมการเป็นจริงได้
ดังนั้น อสมการไม่มีคำตอบเป็นจำนวนจริง
กราฟแสดงคำตอบของอสมการ
เราสามารถนําคําตอบที่ได้ เขียนเป็นกราฟเส้น (line graph) แสดงคําตอบบนเส้นจำนวน เพื่อให้เห็นภาพคําตอบได้ชัดเจน ซึ่งจะประกอบด้วย 3 ส่วนสำคัญ
- จุดโปร่ง(วงกลมโปร่ง) จะหมายถึง จำนวนนั้นไม่เป็นคำตอบ
- จุดทึบ(วงกลมทึบ) จะหมายถึง จำนวนนั้นเป็นคำตอบด้วย
- เส้นทึบที่ลากเชื่อม จะหมายถึง จำนวนที่เป็นคำตอบของอสมการ โดยใช้การลากเส้นผ่านจำนวนนั้น ๆ
ตัวอย่าง
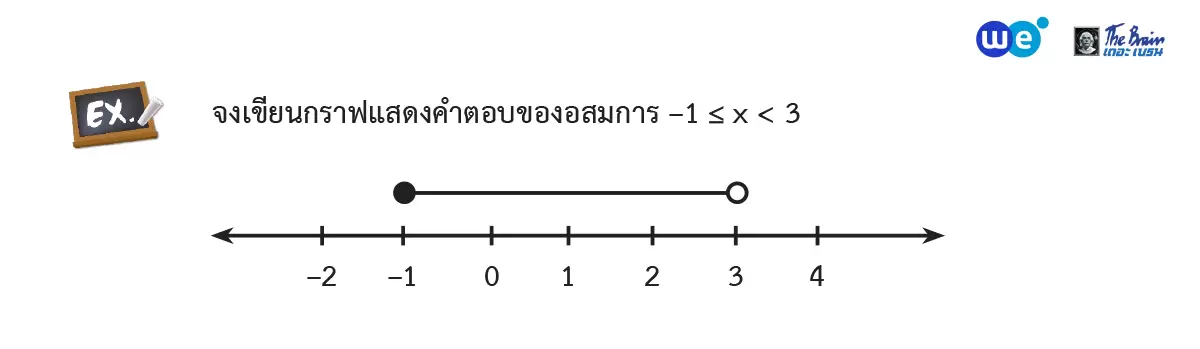
กราฟข้างต้นแสดงจำนวนจริงทุกจำนวนที่มากกว่าหรือเท่ากับ -1 แต่น้อยกว่า 3
ซึ่งเป็นคำตอบของอสมการ -1 ≤ x < 3
เนื่องจาก -1 เป็นคำตอบของอสมการ จะเขียนจุดทึบทับจุดที่แทน -1 ไว้เพื่อแสดงว่า
กราฟรวมจุดที่แทน -1 และเนื่องจาก 3 ไม่ใช่คำตอบของอสมการ ดังนั้นจะเขียนจุดโปร่งตรงจุดที่แทน 3 ไว้เพื่อแสดงว่า กราฟไม่รวมจุดที่แทน 3 และเส้นทึบที่ลากจะหมายถึงจำนวนจริงทั้งหมดที่มีค่าระหว่าง -1 ถึง 3 เป็นคำตอบของอสมการ
วิธีการแก้อสมการเชิงเส้นตัวแปรเดียว
การแก้อสมการ คือ การหาคําตอบของอสมการ ซึ่งทําได้โดยการลองแทนค่าตัวแปร หรือใช้สมบัติการไม่เท่ากันเข้ามาช่วย การลองแทนค่าตัวแปรในอสมการอาจไม่สะดวกเมื่อ อสมการมีความซับซ้อน ดังนั้นเพื่อความรวดเร็วในการแก้อสมการ เราจะใช้สมบัติของการไม่เท่ากันในการหาคําตอบ
สมบัติการบวกของการไม่เท่ากัน
เมื่อ a , b และ c แทนจํานวนจริงใด ๆ
- ถ้า a < b แล้ว a ± c < b ± c
- ถ้า a ≤ b แล้ว a ± c ≤ b ± c
- ถ้า a > b แล้ว a ± c > b ± c
- ถ้า a ≥ b แล้ว a ± c ≥ b ± c
สมบัติการคูณของการไม่เท่ากัน
เมื่อ a , b และ c แทนจํานวนจริงใด ๆ
- ถ้า a < b และ c เป็นจํานวนจริงบวก แล้ว ac < bc
- ถ้า a ≤ b และ c เป็นจํานวนจริงบวก แล้ว ac ≤ bc
- ถ้า a < b และ c เป็นจํานวนจริงลบ แล้ว ac > bc
- ถ้า a ≤ b และ c เป็นจํานวนจริงลบ แล้ว ac ≥ bc
- ถ้า a > b และ c เป็นจํานวนจริงบวก แล้ว ac > bc
- ถ้า a ≥ b และ c เป็นจํานวนจริงบวก แล้ว ac ≥ bc
- ถ้า a > b และ c เป็นจํานวนจริงลบ แล้ว ac < bc
- ถ้า a ≥ b และ c เป็นจํานวนจริงลบ แล้ว ac ≤ bc
น้อง ๆ จะเห็นว่าการคูณด้วยจำนวนบวกอสมการจะไม่เปลี่ยนเครื่องหมาย แต่ถ้าคูณด้วยจำนวนลบอสมการจะเปลี่ยนเครื่องหมาย
และสำหรับการหาคำตอบของอสมการที่มีเครื่องหมาย ≠ จะใช้การแก้สมการมาช่วยในการหาคำตอบ ทำให้ได้คำตอบของอสมการดังกล่าวเป็นจำนวนจริงทุกจำนวน ยกเว้นจำนวนที่เป็นคำตอบของสมการนั้น
ตัวอย่าง

การแก้โจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว
การแก้โจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว จะสร้างอสมการแทนปัญหา แล้วแก้อสมการเพื่อหาคำตอบ เมื่อได้คำตอบแล้ว ต้องนำคำตอบที่ได้ไปตรวจสอบกับเงื่อนไขในโจทย์ปัญหา ว่ามีความสมเหตุสมผลหรือไม่ เนื่องจากคำตอบที่ได้แม้จะเป็นคำตอบของอสมการที่สร้างขึ้น แต่อาจไม่ใช่คำตอบของโจทย์ปัญหา
Steps การแก้โจทย์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียว
Step 1 วิเคราะห์โจทย์เพื่อหาว่าโจทย์ให้หาอะไรและมีเงื่อนไขอะไรบ้าง
Step 2 กําหนดตัวแปรแทนสิ่งที่โจทย์ให้หาหรือแทนสิ่งที่เกี่ยวของกับสิ่งที่โจทย์ให้หา
Step 3 สร้างอสมการตามเงื่อนไขที่โจทย์กำหนด
Step 4 แก้อสมการหาคําตอบ
Step 5 นำคำตอบที่ได้ไปตรวจสอบกับเงื่อนไขที่โจทย์กำหนดมาให้
ตัวอย่างข้อสอบอสมการเชิงเส้นเดียวแปรเดียว
ข้อที่ 1

ข้อที่ 2

ข้อที่ 3

สรุปบทความ
เป็นไงกันบ้างสำหรับวิธีแก้อสมการเชิงเส้นตัวแปรเดียวที่ พี่ภูมิ ได้นำมาฝาก ไม่ยากอย่างที่คิดเลยใช่ไหม ? แต่ถ้าหากน้อง ๆ รู้สึกว่ามีบทเรียนไหนที่ยาก และยังมีความกังวลอยู่ สบายใจได้เลย เพราะการติวคณิตศาสตร์ ม.ต้น และ ติวคณิตศาสตร์ ม.3 ที่ WE BY THE BRAIN จะช่วยปรับพื้นฐานให้น้อง ๆ พร้อมพาตะลุยทำโจทย์ และพิชิตเกรด 4 ให้เอง!
WE BY THE BRAIN ติวเตอร์ตัวตึง ยืน 1 เรื่องติว สอนโดยทีมติวเตอร์ระดับประเทศ พิสูจน์คุณภาพมากว่า 37 ปี จำนวนนักเรียนกว่า 2 ล้านคน สามารถมาเรียนที่ WE BY THE BRAIN ได้เลย พี่ ๆ ติวเตอร์ของเราพร้อมสอนความรู้เข้มข้น แชร์เทคนิคทำข้อสอบจัดเต็ม เรียนจบแล้ว พร้อมลุยทุกสนามสอบแน่นอน!
อัปเดตข่าวสารและสอบถามรายละเอียด เนื้อหาสมการ ม.3 จาก WE BY THE BRAIN ก่อนใครได้ที่
- WE CARE : 02-952-6767
- Line OA : @weplus_care
- Facebook Page : WE BY THE BRAIN
- Instagram : webythebrain
- Twitter : @WEBYTHEBRAIN
- Youtube : WE BY THE BRAIN
โรงเรียนกวดวิชา วี บาย เดอะเบรน เรียนสนุก เข้าใจง่าย ทำโจทย์ได้จริง!

อ.สิทธิเดช เลนุกูล (พี่ภูมิ)
มีความเชี่ยวชาญในการสอนโจทย์คณิตศาสตร์ระดับยาก
ที่คัดสรรจากสนามสอบชั้นนำทั้งในและต่างประเทศ