สวัสดีครับน้อง ๆ พี่ช้าง – อ.มนตรี นิรมิตศิริพงศ์ และ พี่ภูมิ – อ.สิทธิเดช เลนุกูล แท็กทีมมาแจกสรุป ฟังก์ชันตรีโกณมิติ ม.5 ให้ได้อ่านกัน!!
จากที่พี่เคย สรุปเนื้อหาอัตราส่วนตรีโกณมิติ ม.3 ให้น้อง ม.ต้น ทำความเข้าใจและเรียนรู้แนวโจทย์กันไปแล้ว วันนี้ถึงคิวของ “ฟังก์ชันตรีโกณมิติ” ที่เป็นบทเรียนคณิตศาสตร์ระดับชั้น ม.ปลาย บ้างครับ ต้องบอกเลยว่าตรีโกณมิติ ม.5 ขึ้นชื่อว่าเป็นคณิตศาสตร์บทยากอีกหนึ่งบท เพราะมีนิยามใหม่ ๆ ที่ต้องเรียนรู้และสูตรสำคัญที่ต้องจำให้ได้ค่อนข้างเยอะเลยทีเดียว
ถ้าอยากรู้ว่า บทนี้เรียนอะไรบ้าง? จุดไหนสำคัญ? สูตรตรีโกณสูตรไหนต้องจำให้ได้? โจทย์ตรีโกณเป็นยังไง? แนวข้อสอบแต่ละสนามง่าย – ยากประมาณไหน? รวมคำตอบไว้ครบในบทความนี้แล้ว!!
ทบทวนบทเรียนเรื่องฟังก์ชันตรีโกณมิติ
ก่อนอื่นพี่ขอพาน้อง ๆ มาทบทวนบนเรียนเรื่องฟังก์ชันตรีโกณมิติกันสักหน่อยครับ ใครที่ยังไม่รู้ว่า ตรีโกณมิติ คืออะไร? คำว่า “ตรีโกณมิติ” มาจากคำภาษากรีกสองคำ นั่นคือ “trigonon” ที่แปลว่า มุม 3 มุม และคำว่า “metro” ที่แปลว่า การวัด ซึ่งตรีโกณมิติเป็นสาขาหนึ่งของคณิตศาสตร์ ที่ศึกษาความสัมพันธ์ระหว่างความยาวและมุมของรูปสามเหลี่ยม
พื้นฐานเบื้องต้นเกี่ยวกับฟังก์ชันตรีโกณมิติ
อัตราส่วนตรีโกณมิติ
หลังจากทบทวนเกี่ยวกับความหมายและที่มาของคำว่าตรีโกณมิติแล้ว เรามาดูหัวข้อต่อไปอย่าง อัตราส่วนตรีโกณมิติ เลยดีกว่า อัตราส่วนตรีโกณมิติ คือ อัตราส่วนความยาวของ 2 ด้านใด ๆ ในสามเหลี่ยมมุมฉาก
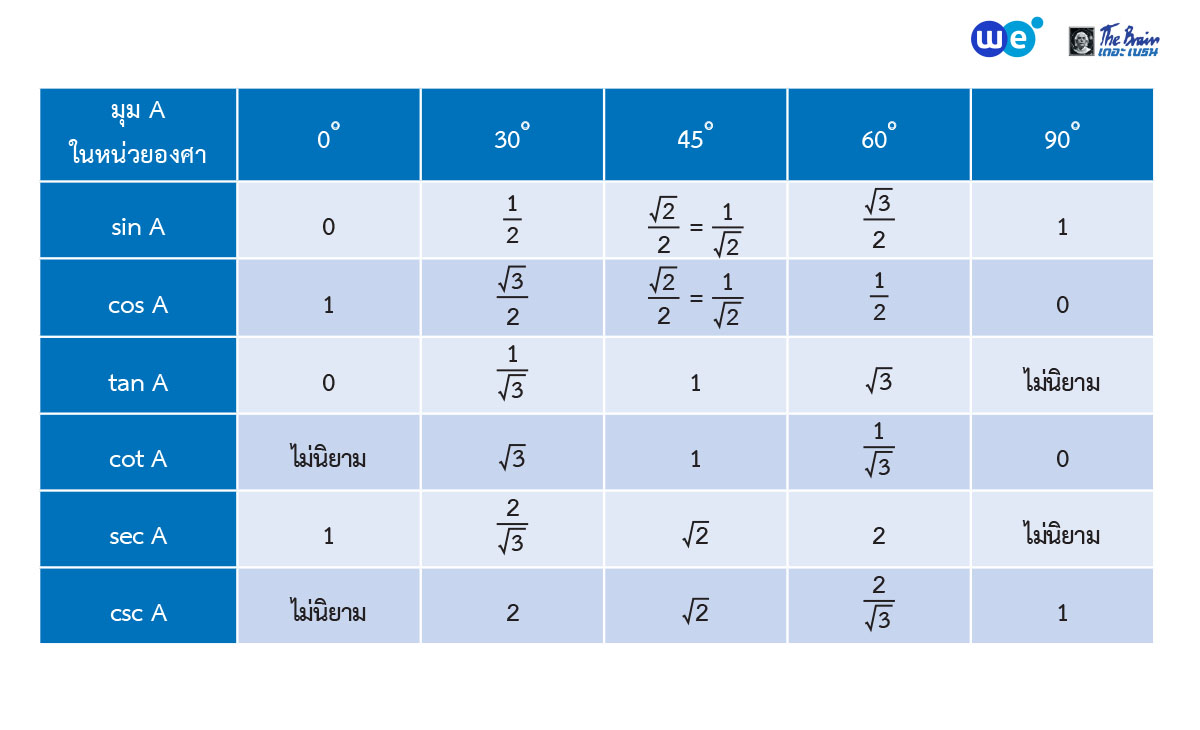
หากพิจารณารูปสามเหลี่ยมมุมฉาก ABC ที่มีมุม C เป็นมุมฉาก
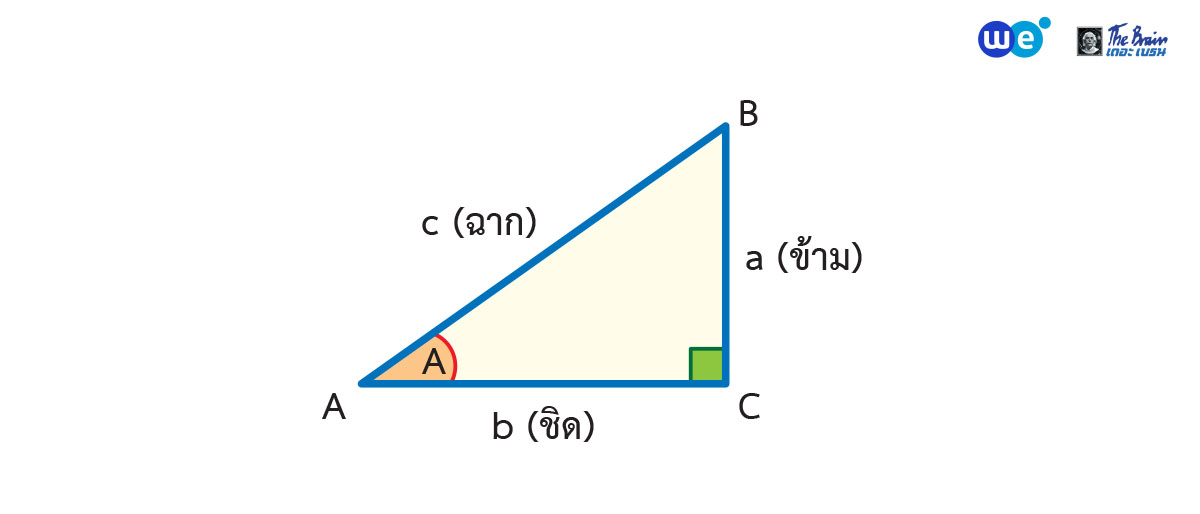
- ด้าน AB เรียกว่า ด้านตรงข้ามมุมฉาก (ฉาก)
- ด้าน BC เรียกว่า ด้านตรงข้ามมุม A (ข้าม)
- ด้าน AC เรียกว่า ด้านประชิดมุม A (ชิด)
ซึ่งอัตราส่วนตรีโกณมิติที่น้อง ๆ ต้องรู้จักมีทั้งหมด 6 อัตราส่วน นั่นคือ

หากลองสังเกตอัตราส่วนตรีโกณมิติด้านบนนี้จะพบว่า มีอัตราส่วนหลัก 3 อัตราส่วนด้วยกัน นั่นคือ ![]() ,
, ![]() และ
และ ![]() พี่แนะนำว่าตอนที่น้อง ๆ ท่องจำก็ให้ท่องแค่ 3 อัตราส่วนนี้ก็พอครับ
พี่แนะนำว่าตอนที่น้อง ๆ ท่องจำก็ให้ท่องแค่ 3 อัตราส่วนนี้ก็พอครับ
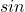 ท่องว่า ข้าม – ฉาก
ท่องว่า ข้าม – ฉาก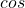 ท่องว่า ชิด – ฉาก
ท่องว่า ชิด – ฉาก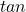 ท่องว่า ข้าม – ชิด
ท่องว่า ข้าม – ชิด
และอีก 3 อัตราส่วนที่เหลือจะเป็นส่วนกลับของ 3 อัตราส่วนแรก จึงได้ว่า
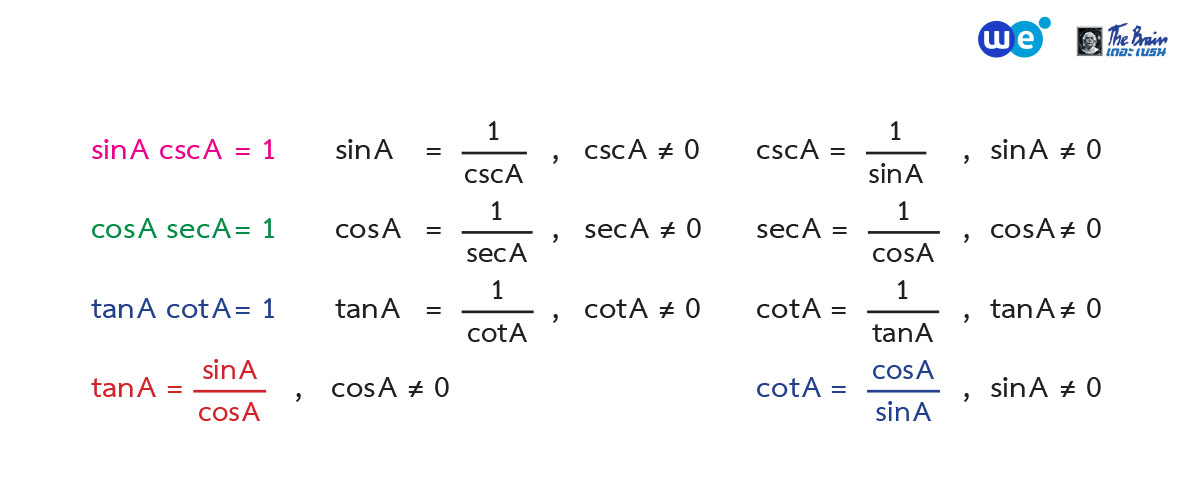
ค่าอัตราส่วนตรีโกณมิติของมุม 0° , 30° , 45° , 60° และ 90°
พอน้อง ๆ ได้รู้จักทั้งอัตราส่วนหลักและส่วนกลับของอัตราส่วนตรีโกณมิติแล้ว ก็จะได้เรียนเรื่อง ค่าอัตราส่วนตรีโกณมิติของมุม 0° , 30° , 45° , 60° และ 90° ตามตารางด้านล่างนี้เลยครับ
สำหรับใครเรียนตรีโกณ ม.ต้น หรือ ม.ปลาย ก็มักจะเจอปัญหาเดิม ๆ ซ้ำ ๆ คือ จำค่าอัตราส่วนตรีโกณมิติไม่ได้ ก็ต้องลองทำตาม เทคนิคการหาค่าอัตราส่วนตรีโกณมิติ ที่ใช้แค่สองมือของเราแบบไม่ต้องง้ออุปกรณ์ ก็ช่วยให้หาค่าตรีโกณมิติได้ภายใน 3 วินาทีเท่านั้น!!
ตัวอย่าง กำหนดให้ ![]()
ถ้า ![]() แล้ว
แล้ว ![]() มีค่าเท่ากับเท่าใด
มีค่าเท่ากับเท่าใด
วิธีทำ เนื่องจาก ![]() และจาก
และจาก ![]() จะได้
จะได้ ![]()
∴ ![]()
โคฟังก์ชัน (Co-function)
เรามาดูหัวข้อต่อไปที่จะได้เรียนกันในบทตรีโกณมิติ ม.5 อย่าง โคฟังก์ชัน (Co-function) เลย สำหรับน้องที่ยังงง ๆ ว่า “โคฟังก์ชัน” มันคืออะไรกันครับเนี่ย?! เดี๋ยวพี่จะอธิบายให้ฟังแบบเข้าใจง่าย ๆ
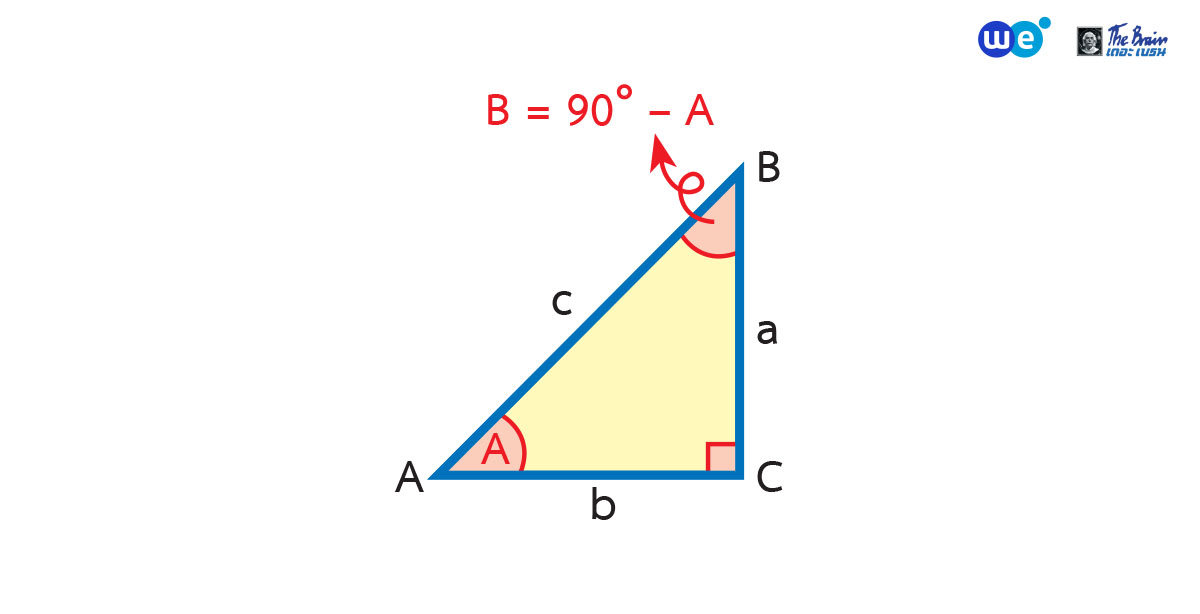
ถ้า ![]() จะได้ว่า
จะได้ว่า
![]()
![]()
![]()
โคฟังก์ชัน คือ การเท่ากันของค่าฟังก์ชันตรีโกณ โดยมีเงื่อนไขว่า มุมรวมกันได้ 90 องศา
แล้ว ![]() เท่ากับ
เท่ากับ ![]()
![]() เท่ากับ
เท่ากับ ![]()
![]() เท่ากับ
เท่ากับ ![]()
ตัวอย่างเช่น
![]()
![]()
![]()
เอกลักษณ์ตรีโกณมิติ
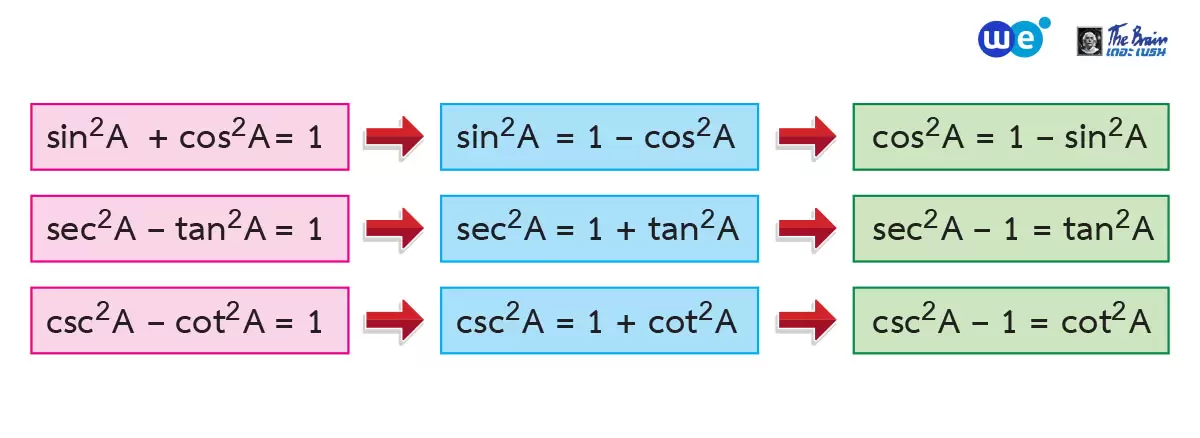
นอกจากจะได้เรียนรู้เกี่ยวกับโคฟังก์ชันแล้ว น้อง ๆ ยังต้องรู้จัก เอกลักษณ์ตรีโกณมิติ ด้วยครับ เอกลักษณ์ตรีโกณมิติ คือ การเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม ซึ่งมีสูตรดังนี้
มุมและหน่วยในการวัดมุม
ในบทฟังก์ชันตรีโกณมิติ ม.5 น้อง ๆ จะได้เรียนเรื่อง มุมและหน่วยในการวัดมุม ที่ขยายความรู้เพิ่มมากขึ้นกว่าที่ได้เรียนมาในระดับชั้น ม.ต้น ซึ่งหน่วยในการวัดมุมที่สำคัญ ๆ ได้แก่
หน่วยองศา 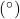
กำหนดให้มุมที่เกิดจากการหมุนส่วนของเส้นตรงไปครบรอบหนหนึ่งมีขนาด 360 องศา และแบ่งหน่วยองศาออกเป็นหน่วยย่อย คือ ลิปดา (′ ) และฟิลิปดา (′′ )
โดยที่ ![]() และ
และ ![]()
หน่วยเรเดียน (R)
สำหรับมุมที่จุดศูนย์กลางของวงกลมที่มีรัศมียาว ![]() หน่วย
หน่วย
ซึ่งรองรับส่วนโค้งที่ยาว ![]() หน่วย จะมีขนาดเท่ากับ
หน่วย จะมีขนาดเท่ากับ ![]() เรเดียน
เรเดียน
และถ้าให้ขนาดของมุมดังกล่าวเป็น ![]() เรเดียน จะได้ว่า
เรเดียน จะได้ว่า
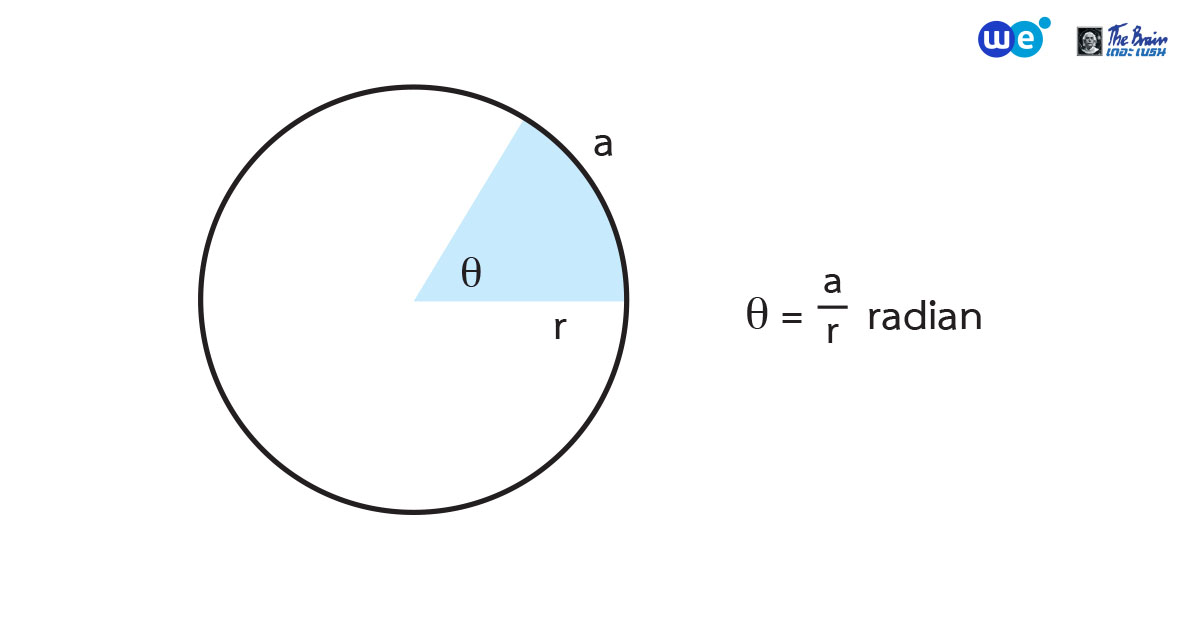
เนื่องจากวงกลมที่มีรัศมียาว ![]() หน่วย จะมีเส้นรอบวงยาว
หน่วย จะมีเส้นรอบวงยาว ![]() หน่วย
หน่วย
มุมที่จุดศูนย์กลางของวงกลมที่รองรับส่วนโค้งที่ยาว ![]() หน่วย จึงมีขนาดเท่ากับ
หน่วย จึงมีขนาดเท่ากับ ![]() เรเดียน
เรเดียน
และจะเห็นว่า มุมที่จุดศูนย์กลางของวงกลมซึ่งรองรับส่วนโค้งที่ยาวเท่ากับรัศมีของวงกลมนั้นเป็นมุมที่มีขนาด 1 เรเดียน นั่นเอง
ความสัมพันธ์ของมุมในหน่วยองศาและหน่วยเรเดียน
เนื่องจากมุมที่จุดศูนย์กลางวงกลม ซึ่งรองรับส่วนโค้งที่ยาว ![]() หน่วย เกิดจากการหมุนรัศมีของวงกลมไปครบหนึ่งรอบ ดังนั้น
หน่วย เกิดจากการหมุนรัศมีของวงกลมไปครบหนึ่งรอบ ดังนั้น
![]() เรเดียน
เรเดียน ![]()
![]() เรเดียน
เรเดียน ![]()
ตัวอย่าง มุมที่มีขนาด 75 องศา มีขนาดกี่เรเดียน
วิธีทำ เนื่องจาก 180 องศา เท่ากับ ![]() เรเดียน
เรเดียน
ดังนั้น 75 องศา เท่ากับ ![]() เรเดียน
เรเดียน ![]() เรเดียน
เรเดียน
ตัวอย่าง มุมที่มีขนาด 2 เรเดียน มีขนาดกี่องศา
วิธีทำ เนื่องจาก ![]() เรเดียน เท่ากับ 180 องศา
เรเดียน เท่ากับ 180 องศา
ดังนั้น 2 เรเดียน เท่ากับ ![]() องศา
องศา ![]() องศา
องศา
วงกลมหนึ่งหน่วย
การกำหนดค่าของฟังก์ชันตรีโกณมิติ ทำได้โดยใช้วงกลมรัศมียาว 1 หน่วย ซึ่งมีจุดศูนย์กลางอยู่ที่จุดกำเนิด วงกลมนี้เป็นกราฟของความสัมพันธ์
![]()
การวัดความยาวส่วนโค้งและการวัดมุมในวงกลมหนึ่งหน่วย
เมื่อเราทำการวัดความยาวส่วนโค้ง โดยเริ่มวัดจากจุด (1, 0) วัดระยะไปตามส่วนโค้งของวงกลมหนึ่งหน่วยให้ยาว 𝛳 หน่วย จะถึงจุด (x, y) (มี (x, y) เป็นจุดปลาย) ซึ่งอยู่บนวงกลมหนึ่งหน่วย โดยมีข้อตกลงสำหรับทิศทางการวัดและเครื่องหมายดังนี้
ถ้าวัดความยาวส่วนโค้งไปใน “ทิศทวนเข็มนาฬิกา” เครื่องหมายของส่วนโค้งจะเป็น “บวก”
ถ้าวัดความยาวส่วนโค้งไปใน “ทิศตามเข็มนาฬิกา” เครื่องหมายของส่วนโค้งจะเป็น “ลบ”
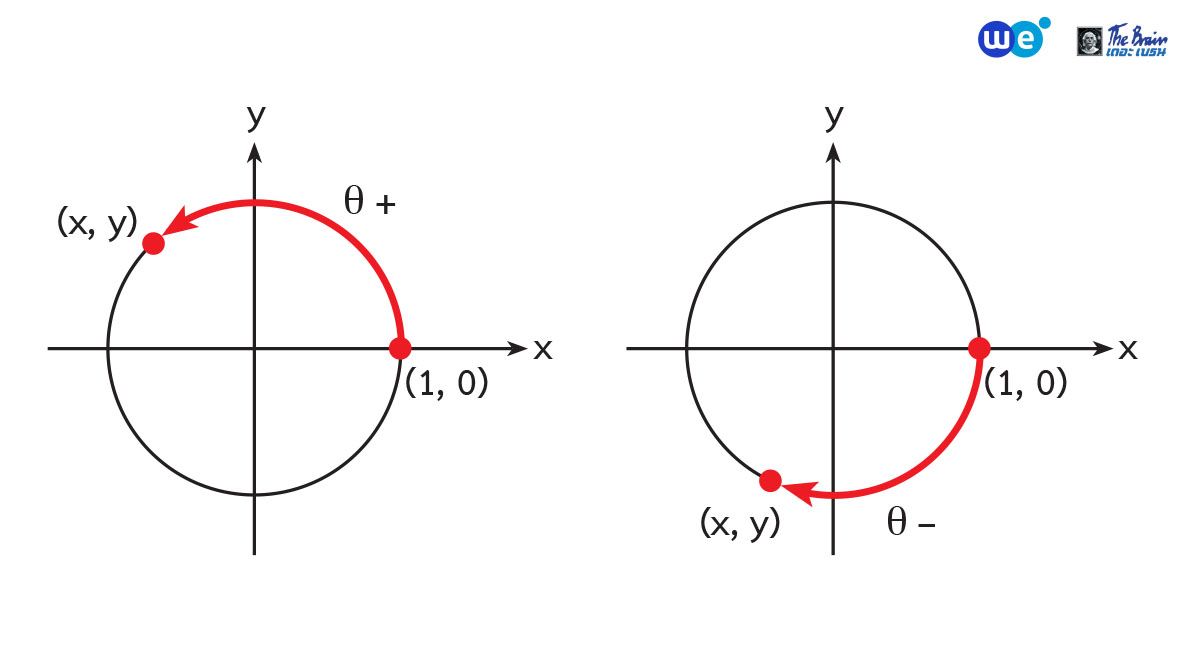
สำหรับการวัดมุมในวงกลมหนึ่งหน่วยก็เช่นเดียวกันครับ
ถ้าวัดมุมไปใน “ทิศทวนเข็มนาฬิกา” เครื่องหมายของมุมจะเป็น “บวก”
ถ้าวัดมุมไปใน “ทิศตามเข็มนาฬิกา” เครื่องหมายของมุมจะเป็น “ลบ”
นิยามของฟังก์ชันตรีโกณมิติบนวงกลมหนึ่งหน่วย
เมื่อ (x, y) เป็นจุดปลายส่วนโค้งที่ยาว 𝛳 ที่วัดจากจุด (1, 0)
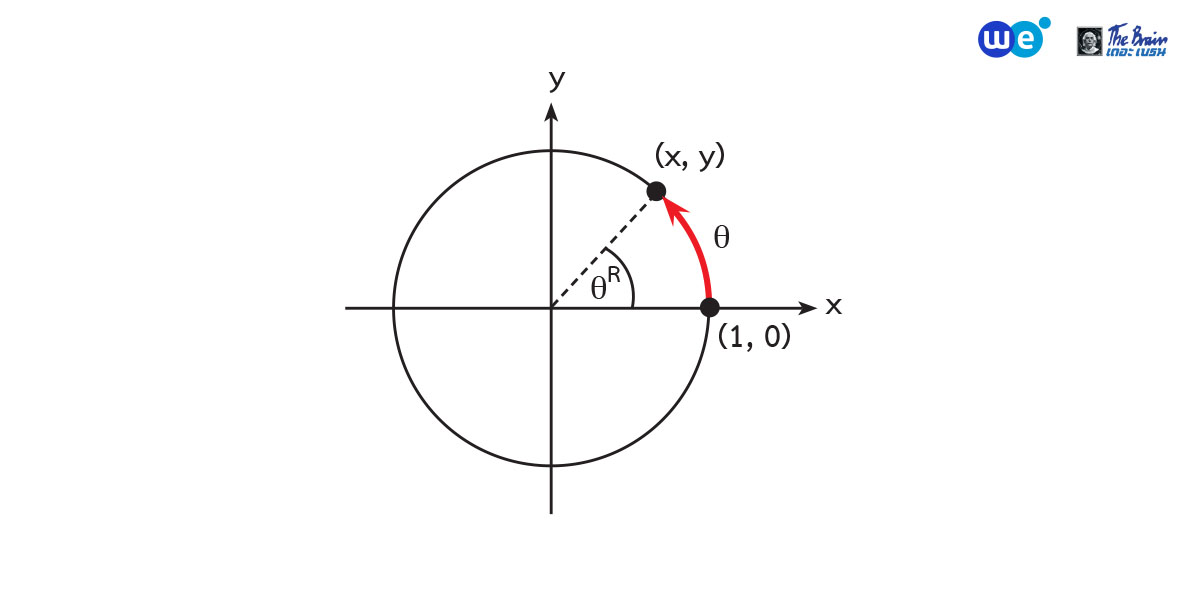
- ฟังก์ชันไซน์ (sine function) = {(𝛳, y) / y = sin𝛳}
- ฟังก์ชันโคไซน์ (cosine function) = {(𝛳, x) / x = cos𝛳}
จะเห็นว่า ![]() และ
และ ![]() ดังนั้น ค่าของฟังก์ชันไซน์และฟังก์ชันโคไซน์เป็นจำนวนจริงตั้งแต่ −1 ถึง 1 นั่นก็คือ เรนจ์ของฟังก์ชันไซน์และฟังก์ชันโคไซน์ คือ เซตของจำนวนจริงตั้งแต่ −1 ถึง 1 และโดเมนของฟังก์ชันทั้งสอง คือ เซตของจำนวนจริง
ดังนั้น ค่าของฟังก์ชันไซน์และฟังก์ชันโคไซน์เป็นจำนวนจริงตั้งแต่ −1 ถึง 1 นั่นก็คือ เรนจ์ของฟังก์ชันไซน์และฟังก์ชันโคไซน์ คือ เซตของจำนวนจริงตั้งแต่ −1 ถึง 1 และโดเมนของฟังก์ชันทั้งสอง คือ เซตของจำนวนจริง
จากวงกลมหนึ่งหน่วยจะเห็นว่า สำหรับ ![]() เป็นจำนวนจริงใด ๆ และ n เป็นจำนวนเต็ม
เป็นจำนวนจริงใด ๆ และ n เป็นจำนวนเต็ม
จะได้ ![]()
![]()
การหาค่าของฟังก์ชันไซน์และโคไซน์ของจำนวนจริงตั้งแต่ 0 ถึง ![]() มีข้อสรุปดังนี้
มีข้อสรุปดังนี้
ให้ ![]() เป็นจำนวนจริง ซึ่ง
เป็นจำนวนจริง ซึ่ง ![]()
![]()
![]()
![]()
![]()
![]()
![]()
กราฟของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติเป็น ฟังก์ชันที่เป็นคาบ (periodic function) นั่นคือเมื่อเรานำมาสร้างกราฟแล้วจะสามารถแบ่งแกน X ออกเป็น ช่วงย่อย ๆ (subinterval) โดยลักษณะกราฟในแต่ละช่วงย่อยมีลักษณะเหมือนกัน และความยาวของช่วงย่อยที่สั้นที่สุดที่มีสมบัติดังกล่าว เราจะเรียกว่า คาบ (period) ยกตัวอย่างเช่น
กราฟของ y = sin x
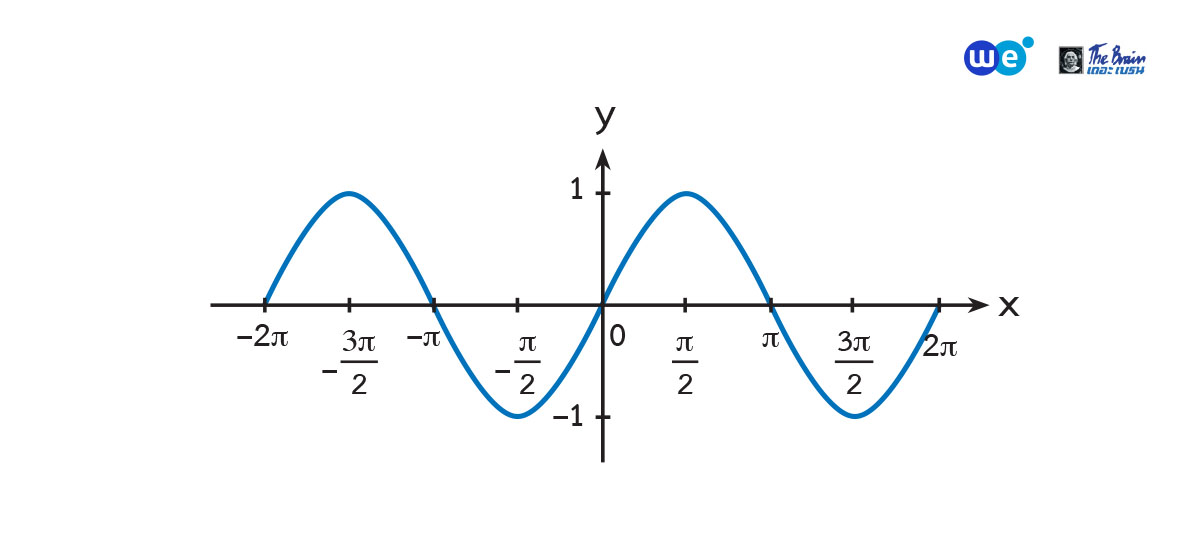
กราฟของ y = cos x
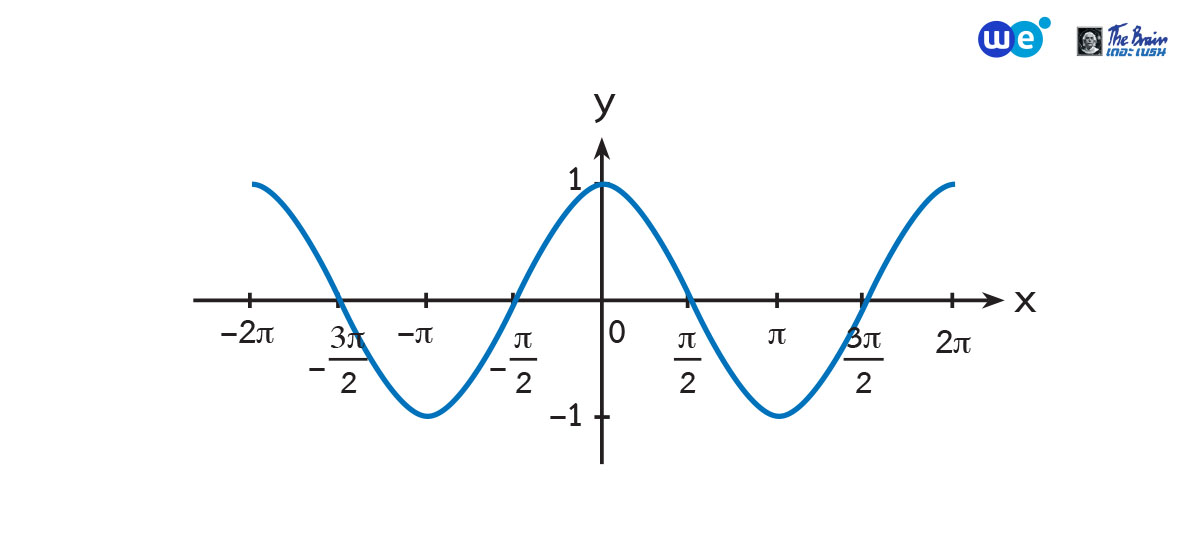
รูปกราฟจะวนกลับมาซ้ำเดิมทุก ๆ ความยาวบนแกน X เท่ากับ ![]()
ดังนั้นกราฟทั้งสองจึงมีคาบเท่ากับ ![]()
สำหรับฟังก์ชันคาบซึ่งมีค่าสูงสุดและค่าต่ำสุด จะเรียกค่าที่เท่ากับครึ่งหนึ่งของผลต่างระหว่างค่าสูงสุดและค่าต่ำสุดของฟังก์ชันนั้นว่า แอมพลิจูด (amplitude)
ดังนั้น ฟังก์ชัน ![]() และ
และ ![]() มีแอมพลิจูดเท่ากับ 1
มีแอมพลิจูดเท่ากับ 1
กราฟของ y = tan x
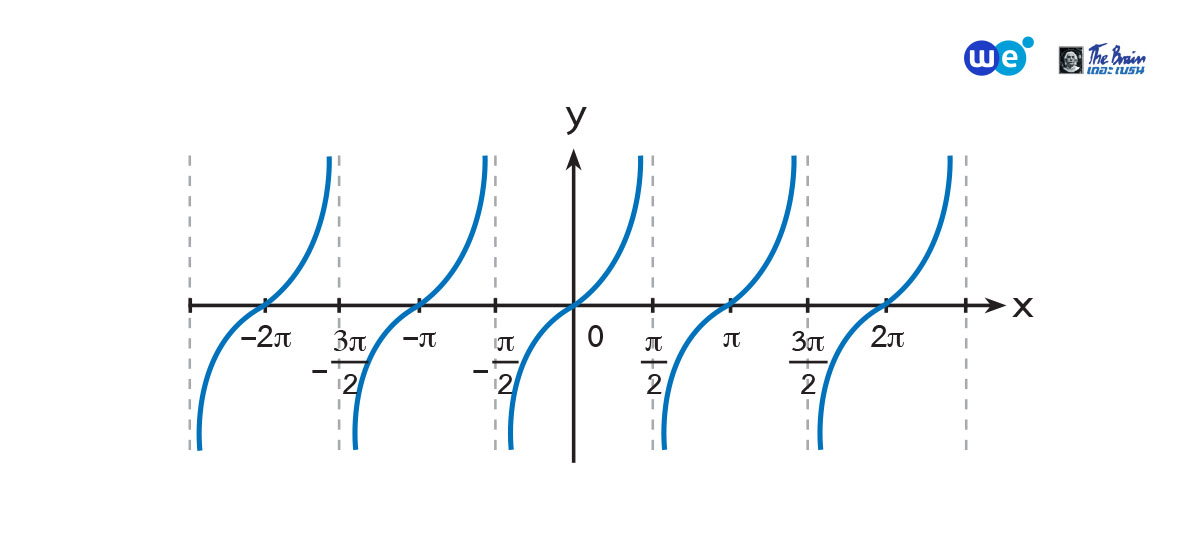
ฟังก์ชันแทนเจนต์เป็นฟังก์ชันที่เป็นคาบ และมีคาบเท่ากับ ![]()
กราฟของ y = cot x
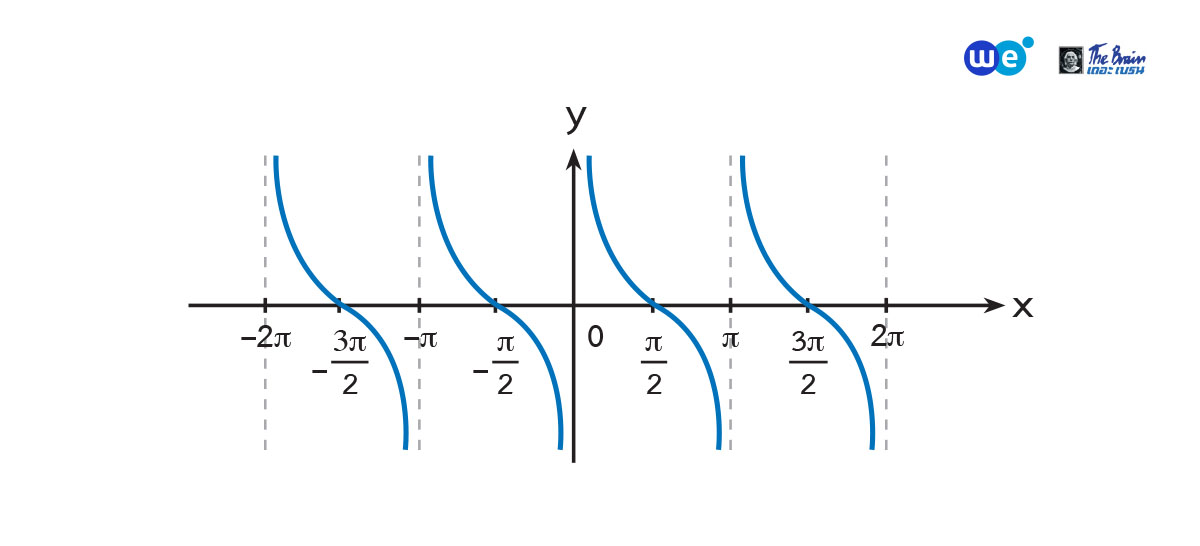
ฟังก์ชันโคแทนเจนต์เป็นฟังก์ชันที่เป็นคาบ และมีคาบเท่ากับ ![]()
กราฟของ y = cosec x
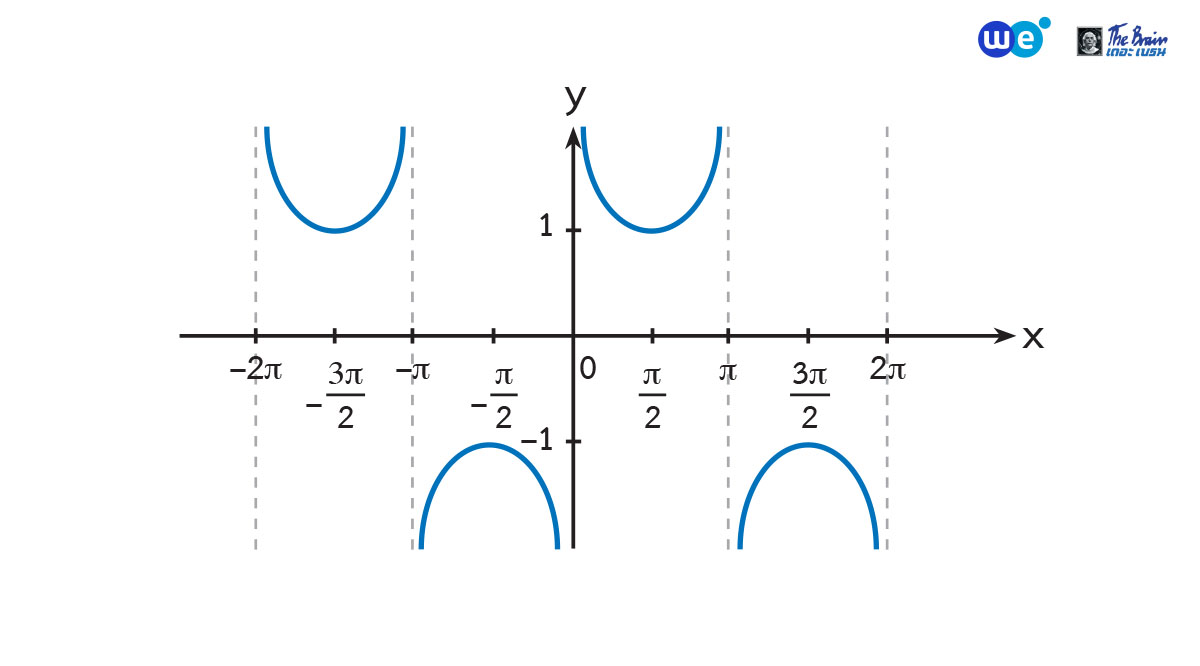
ฟังก์ชันโคเซแคนต์เป็นฟังก์ชันที่เป็นคาบ และมีคาบเท่ากับ ![]()
กราฟของ y = sec x
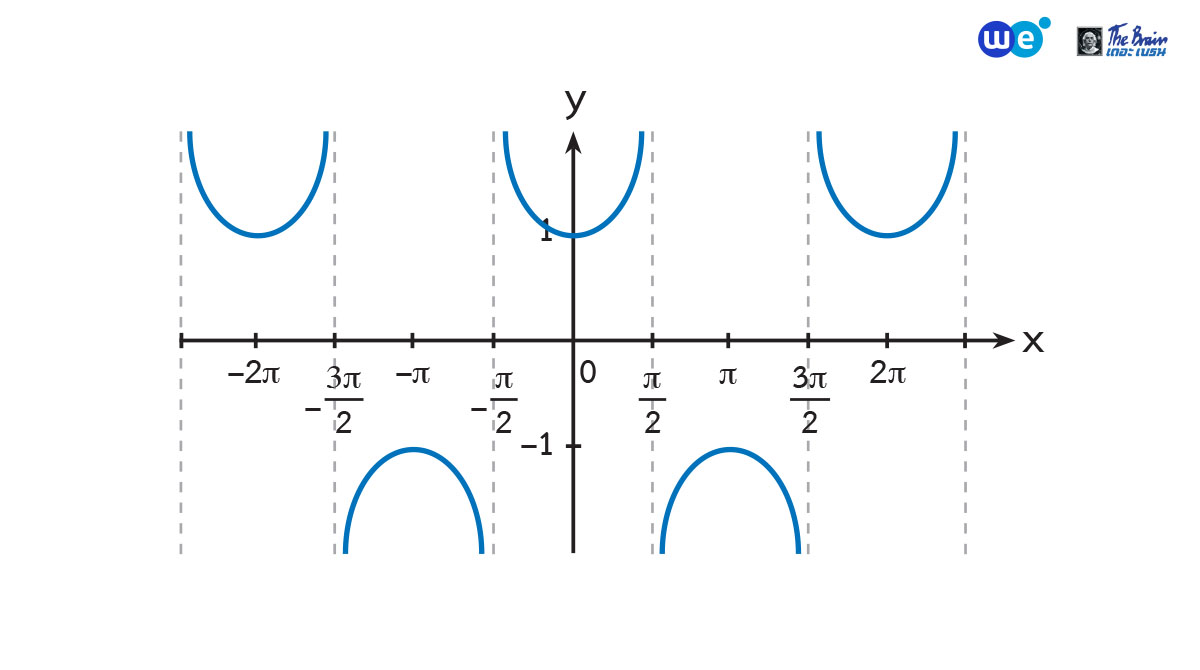
ฟังก์ชันเซแคนต์เป็นฟังก์ชันที่เป็นคาบ และมีคาบเท่ากับ ![]()
สูตรของฟังก์ชันตรีโกณมิติที่ต้องรู้!
ตามที่พี่ได้บอกไปแล้วว่า ฟังก์ชันตรีโกณมิติ ม.5 เป็นคณิตศาสตร์ ม.ปลาย บทปราบเซียนของหลายคน เพราะมีสูตรให้จำเยอะมาก!! พี่เลย สรุปสูตรฟังก์ชันตรีโกณมิติที่ต้องรู้ พร้อมตัวอย่าง ที่จะช่วยให้น้อง ๆ เข้าใจมากขึ้นครับ
สูตรมุมประกอบ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ตัวอย่าง จงหาค่าของ ![]()
วิธีทำ ![]()
![]()
![]()
![]()
สูตรมุม 2 เท่า
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ตัวอย่าง จงหาค่าของ ![]()
วิธีทำ ![]()
![]()
![]()
![]()
สูตรมุม 3 เท่า
![]()
![]()
![]()
![]()
สูตรผลบวก ผลต่าง และผลคูณ
![]()
![]()
![]()
![]()
ตัวอย่าง จงหาค่าของ ![]()
วิธีทำ ![]()
![]()
![]()
![]()
![]()
ใครอยาก ทบทวนเรื่องสูตรตรีโกณมิติ และเรียนรู้เทคนิคแก้โจทย์ฟังก์ชันตรีโกณมิติ จาก “พี่ช้าง – เดอะ เบรน” คลิกดูคลิปด้านล่างนี้เลย!
ตัวผกผันของฟังก์ชันตรีโกณมิติ
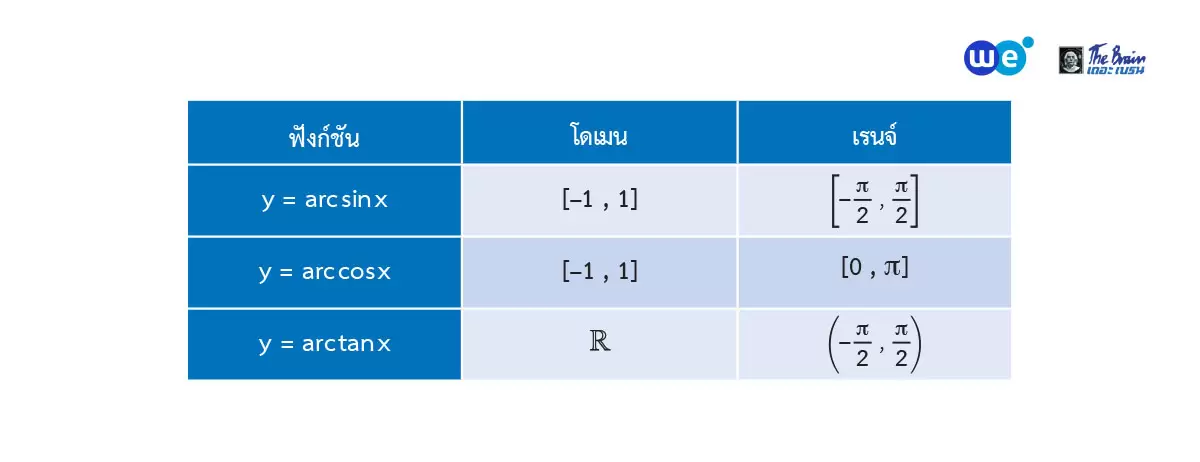
เนื่องจากฟังก์ชันตรีโกณมิติไม่เป็นฟังก์ชัน 1−1 ดังนั้น ตัวผกผันของฟังก์ชันตรีโกณมิติจึงไม่เป็นฟังก์ชัน แต่ถ้าน้อง ๆ กำหนดโดเมนของฟังก์ชันตรีโกณมิติให้เหมาะสมจะพบว่า ตัวผกผันของฟังก์ชันตรีโกณมิติจะเป็นฟังก์ชันครับ
- ฟังก์ชัน
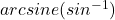 คือ เซตของคู่อันดับ (x, y)
คือ เซตของคู่อันดับ (x, y)
โดยที่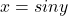 และ
และ 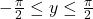
- ฟังก์ชัน
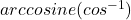 คือ เซตของคู่อันดับ (x, y)
คือ เซตของคู่อันดับ (x, y)
โดยที่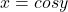 และ
และ 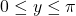
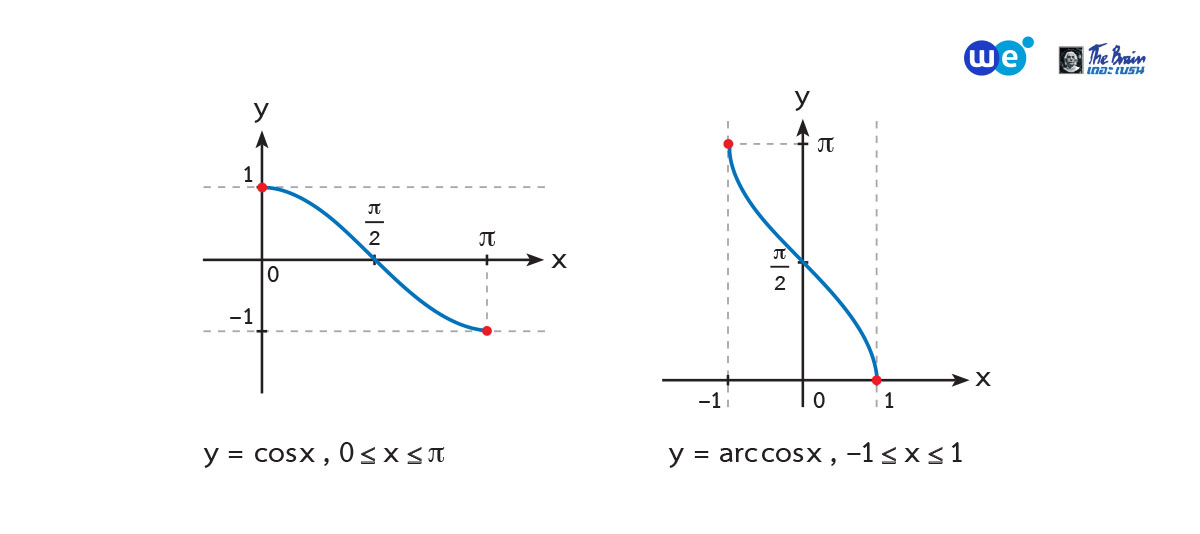
- ฟังก์ชัน
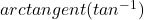 คือ เซตของคู่อันดับ (x, y)
คือ เซตของคู่อันดับ (x, y)
โดยที่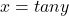 และ
และ 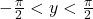
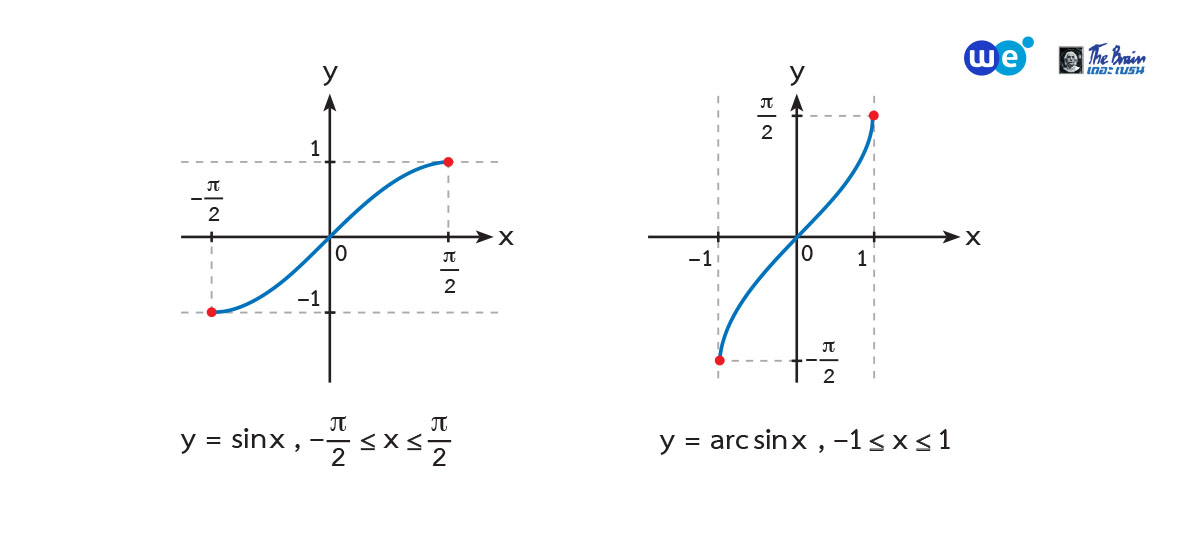
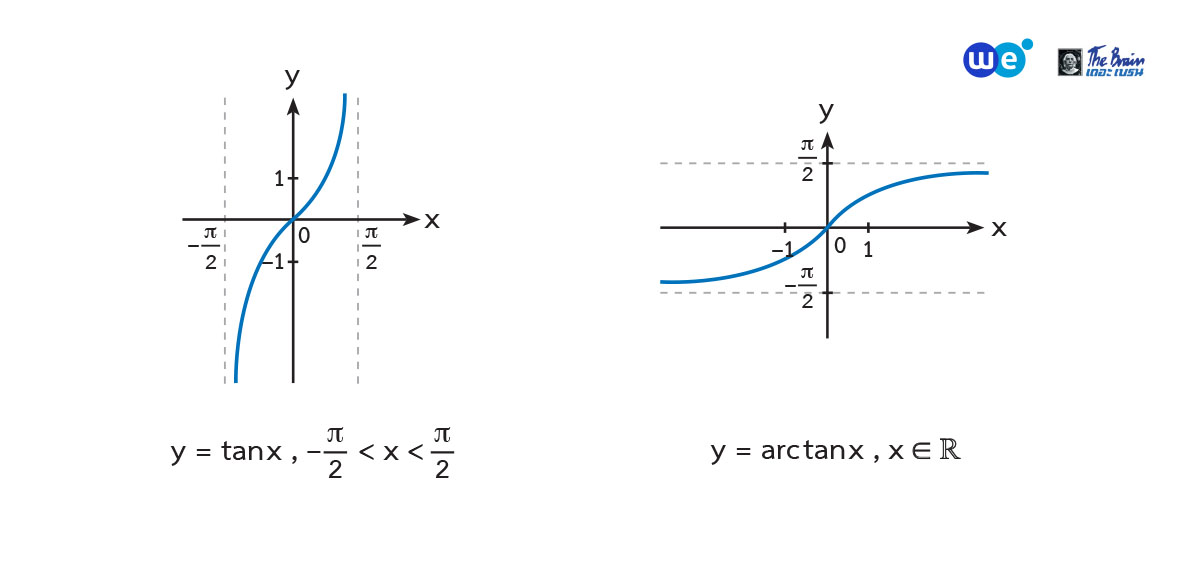
ตัวอย่าง จงหาค่าของ ![]()
วิธีทำ เนื่องจาก ![]()
![]()
ตัวอย่าง จงหาค่าของ ![]()
วิธีทำ ![]()
![]()
การแก้สมการตรีโกณ
การแก้สมการตรีโกณมิติสามารถทำได้ในทำนองเดียวกันกับการแก้สมการทั่วไปครับ โดยน้อง ๆ ต้องอาศัยความรู้เกี่ยวกับฟังก์ชันตรีโกณมิติ เพื่อหาคำตอบของสมการ เนื่องจากฟังก์ชันตรีโกณมิติไม่เป็นฟังก์ชัน 1−1 ค่าของฟังก์ชันตรีโกณมิติของจำนวนจริงหรือมุมใด ๆ อาจจะซ้ำกันได้
ดังนั้น ในการหาคำตอบของสมการ ถ้าโจทย์ไม่ได้กำหนดให้คำตอบอยู่ในช่วงใดช่วงหนึ่งแล้ว คำตอบควรอยู่ในรูปค่าทั่วไปครับ
ตัวอย่าง จงหาคำตอบของ ![]() เมื่อ
เมื่อ ![]()
วิธีทำ จาก ![]()
จะได้ ![]()
นั่นคือ ![]() หรือ
หรือ ![]()
ค่าของ ![]() ในช่วง
ในช่วง ![]() ที่ทำให้
ที่ทำให้ ![]() คือ
คือ ![]() และ
และ ![]()
ค่าของ ![]() ในช่วง
ในช่วง ![]() ที่ทำให้
ที่ทำให้ ![]() คือ
คือ ![]() และ
และ ![]()
ดังนั้น ค่าของ ![]() ในช่วง
ในช่วง ![]() ที่ทำให้สมการเป็นจริง คือ
ที่ทำให้สมการเป็นจริง คือ ![]() ,
, ![]() ,
, ![]() ,
, ![]()
การแก้สามเหลี่ยม ระยะทางและความสูง
และอีกหนึ่งหัวข้อของตรีโกณมิติ ม.5 ที่น้อง ๆ จะได้เรียนกันก็คือ การนำความรู้เรื่องฟังก์ชันตรีโกณมิติมาประยุกต์ใช้ใน การแก้สามเหลี่ยม รวมถึง การหาระยะทางและความสูง ด้วยครับ
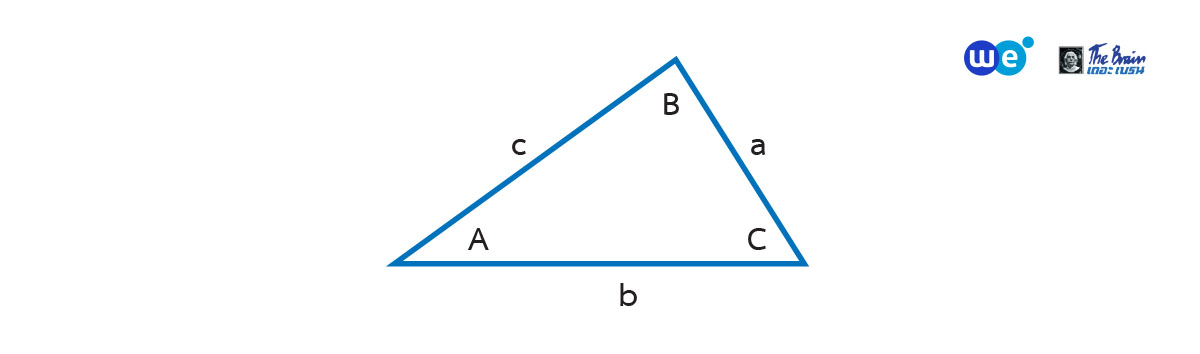
กำหนดให้รูปสามเหลี่ยม ABC มีด้านตรงข้ามมุม A, B และ C ยาว a, b และ c ตามลำดับจะได้
กฎของ sine
![]()
กฎของ cosine
![]()
![]()
![]()
กฎของโปรเจกชัน และพื้นที่สามเหลี่ยม ABC
![]()
![]()
![]()
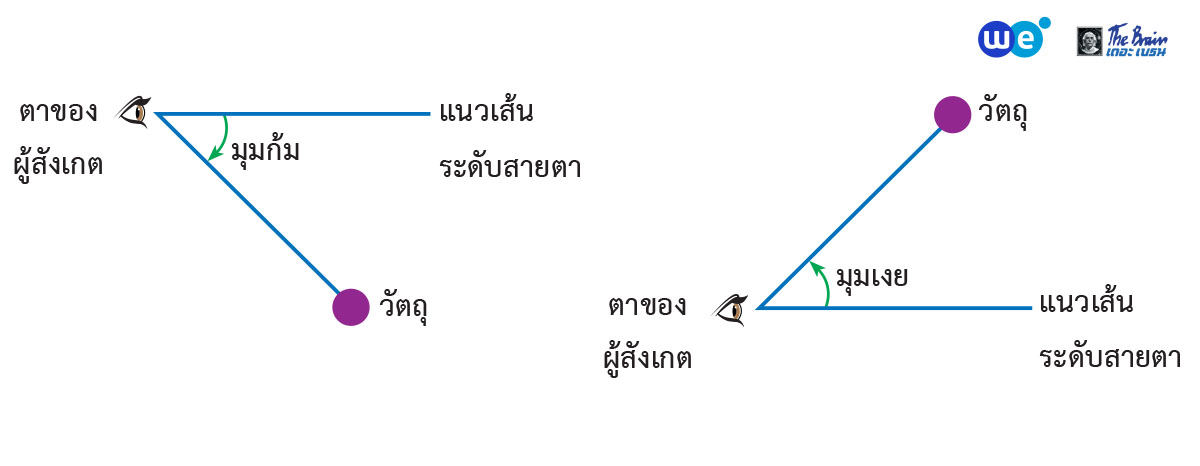
การประยุกต์ของอัตราส่วนตรีโกณมิติ (มุมก้ม / มุมเงย)
“มุมก้ม” และ “มุมเงย” เป็นมุมที่เกิดจากแนวเส้นระดับสายตา และแนวเส้นจากตาไปยังวัตถุ ถ้าวัตถุอยู่ ต่ำกว่า แนวเส้นระดับสายตา มุมที่ได้เรียกว่า มุมก้ม แต่ถ้าวัตถุอยู่ สูงกว่า แนวเส้นระดับสายตา มุมที่ได้เรียกว่า มุมเงย โดยขนาดของมุมก้มและมุมเงยจะเป็น จำนวนจริงบวก เสมอครับ
แนวข้อสอบคณิตศาสตร์ พร้อมเฉลย - ฟังก์ชันตรีโกณมิติ ม.5
เอาล่ะ! หลังจากที่น้อง ๆ อ่านสรุปเนื้อหาฟังก์ชันตรีโกณมิติ ม.5 จบแล้ว คราวนี้เรามาดูโจทย์ตรีโกณกันบ้างดีกว่าว่า แนวข้อสอบของแต่ละสนามสอบเป็นยังไง ระดับความยาก – ง่ายประมาณไหน โดยพี่รวบรวม ข้อสอบคณิตศาสตร์ บทฟังก์ชันตรีโกณมิติ มาให้หลากหลายแนว ทั้งข้อสอบในโรงเรียน ข้อสอบสมาคมคณิตศาสตร์ และข้อสอบเข้ามหาวิทยาลัย ให้น้อง ๆ ได้เรียนรู้วิธีแก้โจทย์แต่ละแบบครับ
1. โจทย์ฟังก์ชันตรีโกณมิติ - ข้อสอบ Midterm / Final

2. โจทย์ฟังก์ชันตรีโกณมิติ - ข้อสอบ A-Level คณิตศาสตร์ประยุกต์ 1

3. โจทย์ฟังก์ชันตรีโกณมิติ - ข้อสอบ PAT1 ความถนัดทางคณิตศาสตร์

4. โจทย์ฟังก์ชันตรีโกณมิติ - ข้อสอบสมาคมคณิตศาสตร์


ติวคณิตศาสตร์ ม.5 กับ WE BY THE BRAIN พร้อมพิชิตเกรด 4
จบไปแล้วนะครับ กับ สรุปฟังก์ชันตรีโกณมิติ ม.5 ที่พี่อัดแน่นความรู้ให้น้อง ๆ แบบไม่มีกั๊ก ทั้งสรุปเนื้อหา สรุปสูตร เน้นจุดสำคัญ แถมยังนำแนวข้อสอบตรีโกณมิติหลากหลายสนามมาฝากกันอีกด้วย
แต่สำหรับใครที่เรียนคณิตศาสตร์ บทตรีโกณมิติ ม.ปลาย แล้วยังไม่ค่อยเข้าใจเนื้อหา หรืออยากเพิ่มความมั่นใจก่อนลงสอบแข่งขันสนามสำคัญ ที่ WE BY THE BRAIN เรามีทั้ง คอร์สคณิตศาสตร์ ม.ปลาย – ฟังก์ชันตรีโกณมิติ และ คอร์สคณิตศาสตร์ ม.5 รวมทุกบท ให้เลือกสมัครเรียนแบบตอบโจทย์ความต้องการของน้อง ๆ ทุกคน
สมัครคอร์สนี้ดียังไง?
✔ พี่ ๆ ติวเตอร์จะปูพื้นฐานให้อย่างละเอียด ด้วยเนื้อหาที่กระชับเข้าใจง่าย
✔ พาน้อง ๆ ฝึกทำโจทย์อย่างเข้มข้นเป็นขั้นตอน ไล่ระดับตั้งแต่ง่าย ปานกลาง ไปจนถึงยาก ที่เป็นข้อสอบแข่งขันจากสนามสอบต่าง ๆ ทั้งในและต่างประเทศ
✔ สอนทำข้อสอบอัตนัยแบบแสดงวิธีทำเป็นขั้นตอน พร้อมเสริมเทคนิคลัดจากพี่ ๆ ติวเตอร์ ที่ช่วยให้ทำข้อสอบปรนัยได้รวดเร็วยิ่งขึ้น
✔ คอร์สนี้เหมาะสำหรับน้อง ๆ ที่ต้องการพิชิตเกรด 4 วิชาคณิตศาสตร์ และเป็นพื้นฐานสำคัญในการเตรียมสอบเข้ามหาวิทยาลัยในระบบ TCAS
คำถามที่พบบ่อย (FAQ) เกี่ยวกับ “บทฟังก์ชันตรีโกณมิติ”
บทฟังก์ชันตรีโกณมิติ เชื่อมโยงกับคณิตศาสตร์บทไหนบ้าง?
ฟังก์ชันตรีโกณมิติเป็นบทที่ต่อยอดมาจากอัตราส่วนตรีโกณมิติ ม.ต้น โดยเป็นการมองแบบฟังก์ชัน ดังนั้น น้อง ๆ จะต้องมีพื้นฐานเกี่ยวกับฟังก์ชันมาในระดับหนึ่งครับ
และบทฟังก์ชันตรีโกณมิติ ม.5 ยังต่อยอดไปยังคณิตศาสตร์ ม.ปลาย บทอื่น ๆ นั่นคือ เวกเตอร์ และ จำนวนเชิงซ้อน ถ้าน้องเรียนบทนี้เข้าใจอย่างถ่องแท้ อีก 2 บทที่เหลือก็จะเป็นเรื่องง่ายในทันที
เคล็ดลับเรียนตรีโกณมิติ ม.5 เปลี่ยนบทยากให้เป็นเรื่องเข้าใจง่าย
ความยากของบทฟังก์ชันตรีโกณมิติ ม.5 จะอยู่ที่สูตรและนิยามใหม่ ๆ ที่น้องจะได้เรียนรู้กัน ซึ่งวิธีการที่จะทำให้เรียนบทนี้อย่างเข้าใจและไม่เกลียดมัน อย่างแรกเลยคือการทำความเข้าใจนิยามก่อน ถ้าอ่านเองแล้วไม่สามารถเข้าใจได้ก็ต้องหาตัวช่วยครับ จะเป็นคุณครู เพื่อน ๆ หรือพี่ ๆ ติวเตอร์ ให้เขาช่วยอธิบายให้เราเข้าใจ (บทนี้นิยามของเขาไม่ได้เข้าใจยากจริง ๆ นะ 🤞)
หลังจากนั้นค่อย ๆ ทำโจทย์ เก็บจากง่าย ๆ เพื่อให้เราใช้สูตรเป็น แล้วค่อยขยับไปทำโจทย์ยาก ๆ เพื่อให้รู้จักประยุกต์สูตรและใช้สูตรแบบผสม ก็จะช่วยให้เราสนุกกับการเรียนฟังก์ชันตรีโกณมิติ และเรียนบทนี้เข้าใจง่ายขึ้น
บทฟังก์ชันตรีโกณมิติ ข้อสอบชอบออกแนวไหน?
โจทย์ฟังก์ชันตรีโกณมิติจะออกครอบคลุมทุกหัวข้อที่ได้เรียนไป แต่สิ่งที่น้อง ๆ ต้องระวัง คือ เรื่องเครื่องหมายของฟังก์ชันตรีโกณมิติ และขอบเขตของการหาค่าของฟังก์ชันตรีโกณมิติ ครับ
ใครอยากเก่งคณิต อยากได้โจทย์และเทคนิคดี ๆ จาก พี่ ๆ ติวเตอร์ ทีมคณิตศาสตร์ รีบกดติดตามก่อนใครได้ที่ช่องทางด้านล่างนี้เลย!
- Facebook Page : WE BY THE BRAIN
- Instagram : webythebrain
- Youtube : WE BY THE BRAIN
- Tiktok : คณิต เดอะเบรน
- Lemon8 : คณิต เดอะเบรน

อ.มนตรี นิรมิตศิริพงศ์ (พี่ช้าง)
ผู้นำทีมคณิตศาสตร์ของ WE BY THE BRAIN ประสบการณ์การสอน 37 ปี การันตีด้วยการสอนนักเรียนให้สอบติดมหาวิทยาลัยชั้นนำมาแล้วหลายแสนคน

อ.สิทธิเดช เลนุกูล (พี่ภูมิ)
มีความเชี่ยวชาญในการสอนโจทย์คณิตศาสตร์ระดับยาก
ที่คัดสรรจากสนามสอบชั้นนำทั้งในและต่างประเทศ