จำนวนจริง ม.4 เป็นหัวข้อที่น้อง ๆ จะได้เรียนกันมาบ้างแล้วในเนื้อหาคณิตศาสตร์ ม.ต้น ไม่ว่าจะเป็นเรื่องจำนวนนับ, จำนวนเต็ม, จำนวนตรรกยะ, จำนวนอตรรกยะ, การแก้สมการพหุนามต่าง ๆ, เรื่องค่าสัมบูรณ์ นั่นเองครับ
ซึ่งเนื้อหาของระดับชั้น ม.ปลาย จะละเอียดขึ้นและลึกลงไปมากกว่าจำนวนจริง ม.ต้น โดยจะสอนให้น้อง ๆ รู้จักจำนวนชนิดต่าง ๆ รวมทั้งการแก้สมการและอสมการหลากหลายรูปแบบ จึงจัดว่าเป็นพื้นฐานที่สำคัญสำหรับการเรียนต่อในบทอื่น ๆ ของคณิตศาสตร์ ม.ปลาย เช่น ความสัมพันธ์และฟังก์ชัน, ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม, ฟังก์ชันตรีโกณมิติ เป็นต้น
ถ้าอยากรู้ว่าในบทระบบจำนวนจริงจะได้เรียนเกี่ยวกับอะไร มีหัวข้อไหนน่าสนใจบ้าง และแนวข้อสอบมีความยาก – ง่ายประมาณไหน ก็ตามมาดู สรุปเนื้อหาจำนวนจริง ม.4 ที่ “พี่เอ๋ – อ.วิเศษ กี่สุขพันธ์” นำมาฝากกันเลยครับ
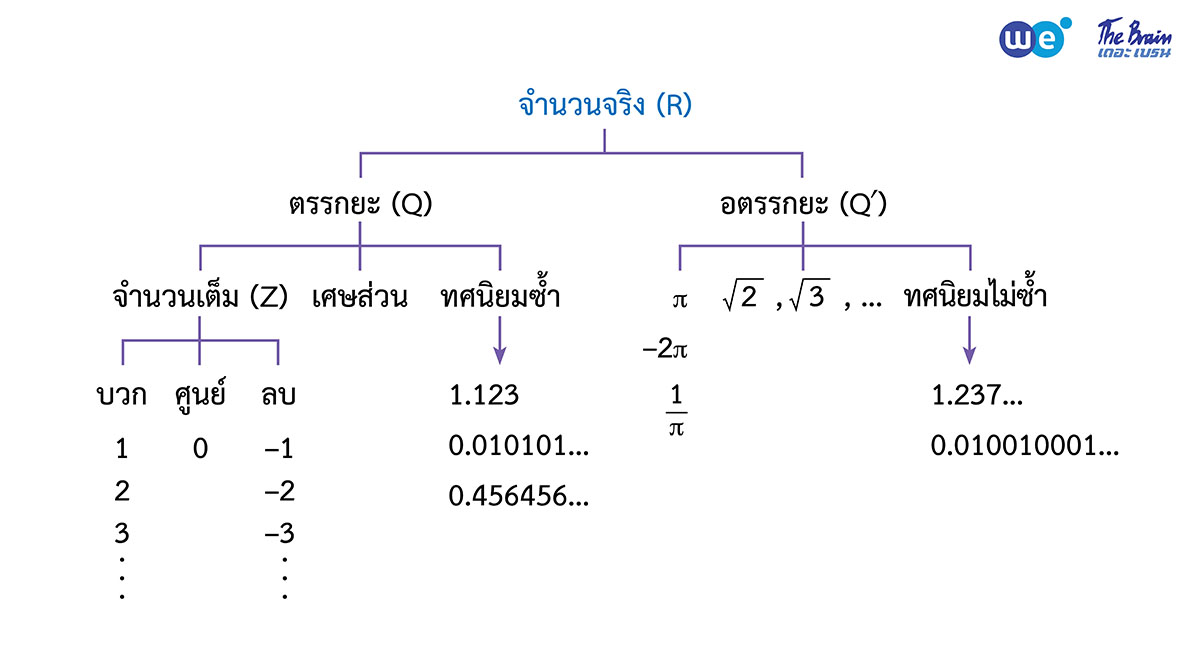
โครงสร้างของระบบจำนวนจริง
หัวข้อแรกของบทจำนวนจริง ม.4 ที่น้อง ๆ จะได้เรียนกัน ก็คือ โครงสร้างของระบบจำนวนจริง ตามแผนผังแสดงความสัมพันธ์ของจำนวนชนิดต่าง ๆ ด้านล่างนี้ครับ
สมบัติของระบบจำนวนจริง
หัวข้อต่อมาน้อง ๆ จะได้เรียนรู้เกี่ยวกับ สมบัติของจำนวนจริง โดยสมบัติสำคัญที่ควรจำให้ได้มีดังนี้
สมบัติปิด
- สมบัติปิดการบวก
ถ้า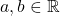 แล้ว
แล้ว 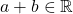
- สมบัติปิดการคูณ
ถ้า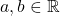 แล้ว
แล้ว 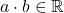
สมบัติการสลับที่
- สมบัติการสลับที่การบวก
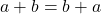
- สมบัติการสลับที่การคูณ
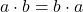
สมบัติการเปลี่ยนกลุ่ม
- สมบัติการเปลี่ยนกลุ่มการบวก
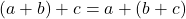
- สมบัติการเปลี่ยนกลุ่มการคูณ
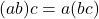
สมบัติการมีเอกลักษณ์
- สมบัติการมีเอกลักษณ์การบวก
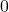 เป็นเอกลักษณ์การบวก
เป็นเอกลักษณ์การบวก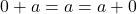
- สมบัติการมีเอกลักษณ์การคูณ
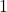 เป็นเอกลักษณ์การคูณ
เป็นเอกลักษณ์การคูณ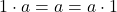
สมบัติการมีอินเวอร์ส
- สมบัติการมีอินเวอร์สการบวก
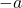 เป็นอินเวอร์สบวกของ
เป็นอินเวอร์สบวกของ 
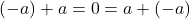
- สมบัติการมีอินเวอร์สการคูณ
 เป็นอินเวอร์สคูณของ
เป็นอินเวอร์สคูณของ 
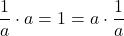 เมื่อ
เมื่อ 
สมบัติการแจกแจง
- สมบัติการแจกแจงการบวกและการคูณ
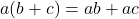
สมบัติปิด
เมื่อนำสมาชิกใด ๆ ในเซตมากระทำกันแล้ว ผลลัพธ์ที่ได้ยังคงเป็นสมาชิกในเซตนั้นเสมอ ถือว่ามีสมบัติปิด เช่น
เซตของจำนวนจริงมีสมบัติปิดการบวก และสมบัติปิดการคูณ
เพราะจำนวนจริง 2 จำนวนใด ๆ มาบวกหรือคูณกัน ผลลัพธ์ที่ได้เป็นจำนวนจริงเสมอ
แต่เซตของจำนวนอตรรกยะไม่มีสมบัติปิดการบวก และไม่มีสมบัติปิดการคูณ
เพราะมีจำนวนอตรรกยะบางคู่ที่บวก , คูณกันแล้วผลลัพธ์ไม่ใช่จำนวนอตรรกยะ เช่น
![]() โดย 0 ไม่เป็นจำนวนอตรรกยะ
โดย 0 ไม่เป็นจำนวนอตรรกยะ
![]() โดย 2 ไม่เป็นจำนวนอตรรกยะ
โดย 2 ไม่เป็นจำนวนอตรรกยะ
เอกลักษณ์ “e * a = a = a * e”
เอกลักษณ์ คือ จำนวนที่ไปกระทำกับจำนวนใด ๆ ก็ตามในเซต แล้วได้ผลลัพธ์เท่ากับ ![]() เดิม
เดิม
![]() เมื่อ
เมื่อ ![]() แสดงว่า เอกลักษณ์การบวกของจำนวนจริงใด ๆ คือ 0
แสดงว่า เอกลักษณ์การบวกของจำนวนจริงใด ๆ คือ 0
![]() เมื่อ
เมื่อ ![]() แสดงว่า เอกลักษณ์การคูณของจำนวนจริงใด ๆ คือ 1
แสดงว่า เอกลักษณ์การคูณของจำนวนจริงใด ๆ คือ 1
อินเวอร์ส “เมื่ออินเวอร์สสำหรับ * ของ a คือ x แล้ว x * a = e = a * x”
อินเวอร์สของ ![]() กระทำกับ
กระทำกับ ![]() จะได้ผลลัพธ์เป็นเอกลักษณ์ เช่น
จะได้ผลลัพธ์เป็นเอกลักษณ์ เช่น
![]()
จะพบว่า ![]() เป็นอินเวอร์สการบวกของ
เป็นอินเวอร์สการบวกของ ![]()
![]()
จะพบว่า ![]() เป็นอินเวอร์สการบวกของ
เป็นอินเวอร์สการบวกของ ![]()
เซตใดจะมีสมบัติอินเวอร์ส เซตนั้นต้องมีเอกลักษณ์ และสมาชิกทุกตัวในเซตต้องหาอินเวอร์สได้ อีกทั้งอินเวอร์สที่หาได้ต้องอยู่ในเซตเดิมเสมอ
ทฤษฎีบทเศษเหลือ
“ ตัวหารเป็นพหุนามดีกรี 1 และเศษเป็นตัวเลขเสมอ ”
หารพหุนาม ![]() ด้วย
ด้วย ![]() เศษตอบ
เศษตอบ ![]()
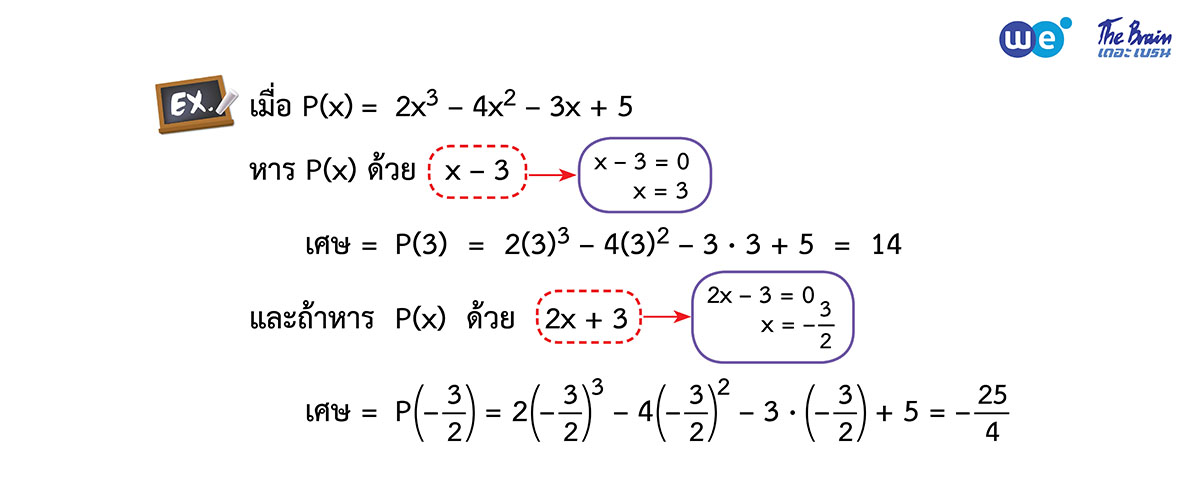
การหารพหุนามแบบขั้นตอนวิธีการหาร
“ นิยมใช้เมื่อเจอโจทย์ที่ตัวหารเป็นพหุนามดีกรีมากกว่า 1 ”

เศษ ![]() จะมีดีกรีน้อยกว่า ตัวหาร
จะมีดีกรีน้อยกว่า ตัวหาร ![]() เสมอ
เสมอ
การหารสังเคราะห์
“ ตัวหารต้องเป็นพหุนามดีกรี 1 ที่มี ส.ป.ส หน้า ![]() เป็น 1 ”
เป็น 1 ”

Note ถ้าใช้หารสังเคราะห์ในกรณี ส.ป.ส หน้า ![]() ของตัวหาร ไม่ใช่ 1 เศษตอบได้เลย แต่ผลหารให้นำไปหารด้วย ส.ป.ส. หน้า
ของตัวหาร ไม่ใช่ 1 เศษตอบได้เลย แต่ผลหารให้นำไปหารด้วย ส.ป.ส. หน้า ![]() ของตัวหารก่อน แล้วค่อยตอบ
ของตัวหารก่อน แล้วค่อยตอบ

สมการกำลัง 2
รูปแบบ ![]() โดย
โดย ![]()
วิธีที่ 1
ถ้า ![]() แยกเป็น 2 วงเล็บได้ ก็ให้แยกเป็นสองวงเล็บ
แยกเป็น 2 วงเล็บได้ ก็ให้แยกเป็นสองวงเล็บ
เช่น จงแก้สมการ ![]()
![]()
![]()
![]() ,
, ![]()
วิธีที่ 2
ใช้สูตร โดย ![]()
ซึ่ง 1) จะมี 2 คำตอบที่เป็นจำนวนจริงที่แตกต่างกัน เมื่อ ![]()
2) จะมี 1 คำตอบ (มองว่ารากซ้ำกัน 2 ตัว) ที่เป็นจำนวนจริง เมื่อ ![]()
3) จะมี 2 คำตอบแต่ไม่ใช่จำนวนจริง เมื่อ ![]()
ทฤษฎีบทตัวประกอบ
พหุนาม ![]() จะมี
จะมี ![]() เป็นตัวประกอบ ก็ต่อเมื่อ
เป็นตัวประกอบ ก็ต่อเมื่อ ![]()
การแยกตัวประกอบ
ให้ ![]() เมื่อ
เมื่อ ![]()
แบบที่ 1 : สัมประสิทธิ์ของพจน์ที่มีกำลังสูงสุดเป็น 1 ![]()
1. หาตัวประกอบของ ![]() ทั้งหมด (ทั้งจำนวนบวกและลบ)
ทั้งหมด (ทั้งจำนวนบวกและลบ)
2. ถ้า ![]() เป็นตัวประกอบของ
เป็นตัวประกอบของ ![]() ซึ่งทำให้
ซึ่งทำให้ ![]() จะได้
จะได้
![]() เป็นตัวประกอบของ
เป็นตัวประกอบของ ![]()
3. เข้าสู่กระบวนการหารสังเคราะห์

แบบที่ 2 : สัมประสิทธิ์ของพจน์ที่มีกำลังสูงสุดไม่เป็น 1 ![]()
1. หาตัวประกอบของ ![]() แล้วให้เป็น
แล้วให้เป็น ![]()
หาตัวประกอบของ ![]() แล้วให้เป็น
แล้วให้เป็น ![]()
2. ถ้า ![]() เป็นเศษส่วนอย่างต่ำ ซึ่งทำให้
เป็นเศษส่วนอย่างต่ำ ซึ่งทำให้ ![]() จะได้
จะได้
![]() เป็นตัวประกอบของ
เป็นตัวประกอบของ ![]()
3. เข้าสู่กระบวนการหารสังเคราะห์

ผลบวกและผลคูณของคำตอบทั้งหมด (Viete)



เพิ่มเติม
กรณี ![]()
![]()
เราได้ว่า ถ้าคำตอบทั้งหมด คือ ![]()
![]() และ
และ ![]()
เรายังได้อีกว่า ![]()
สมการเศษส่วนของพหุนาม
เศษส่วนของพหุนาม
ให้ ![]() และ
และ ![]() เป็นพหุนามโดยที่
เป็นพหุนามโดยที่ ![]()
จะเรียก ![]() ว่าเศษส่วนของพหุนาม
ว่าเศษส่วนของพหุนาม
ที่มี ![]() เป็นตัวเศษ และ
เป็นตัวเศษ และ ![]() เป็นตัวส่วน
เป็นตัวส่วน
เช่น ![]() เมื่อ
เมื่อ ![]()
หรือ ![]() เมื่อ
เมื่อ ![]()

การบวก, การลบ, การคูณและการหารเศษส่วนของพหุนาม
1. ![]() ,
, ![]()
2. ![]() ,
, ![]()
3. ![]() ,
, ![]() และ
และ ![]()
4. ![]() ,
, ![]() ,
, ![]() และ
และ ![]()
![]()
สมการเศษส่วนของพหุนาม
สมการเศษส่วนของพหุนาม คือ สมการที่สามารถจัดอยู่ในรูป
![]() ,
, ![]()
โดยเซตคำตอบของ ![]() คือ เซตของจำนวนจริง
คือ เซตของจำนวนจริง ![]()
ซึ่ง ![]() และ
และ ![]()
เทคนิคการแก้อสมการตัวแปรเดียว
ขั้นที่ 1
จัดอสมการให้อยู่ในรูป
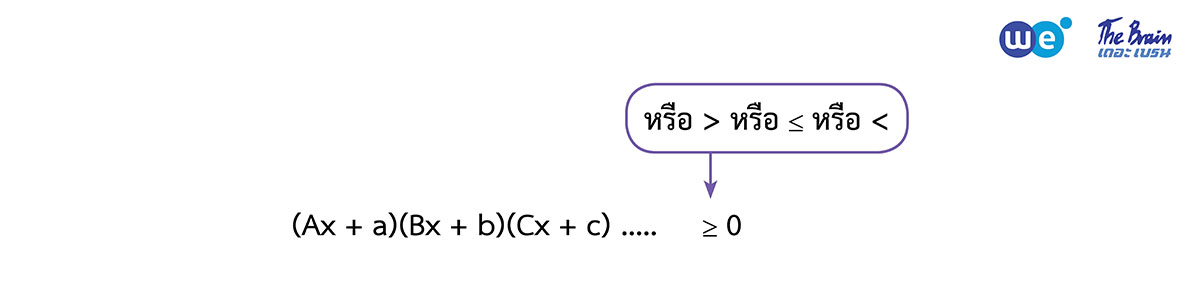
ซ้ายมือ เป็นวงเล็บของ ![]() ดีกรี 1 คูณกัน
ดีกรี 1 คูณกัน
โดยสัมประสิทธิ์หน้า ![]() ต้องเป็นบวก
ต้องเป็นบวก ![]()
ขวามือ ต้องเป็น 0
หมายเหตุ หากสัมประสิทธิ์หน้า ![]() ติดลบ ให้คูณทั้งสองข้างของอสมการด้วย -1 และกลับเครื่องหมายอสมการเป็นตรงข้ามด้วย (ถ้ามีมากกว่า 1 วงเล็บ คู่วงเล็บเครื่องหมายสุดท้ายจะเหมือนเดิม คี่วงเล็บเครื่องหมายสุดท้ายจะเปลี่ยนเป็นตรงข้าม)
ติดลบ ให้คูณทั้งสองข้างของอสมการด้วย -1 และกลับเครื่องหมายอสมการเป็นตรงข้ามด้วย (ถ้ามีมากกว่า 1 วงเล็บ คู่วงเล็บเครื่องหมายสุดท้ายจะเหมือนเดิม คี่วงเล็บเครื่องหมายสุดท้ายจะเปลี่ยนเป็นตรงข้าม)
ขั้นที่ 2
จับแต่ละวงเล็บเท่ากับ 0 จะได้ค่า ![]() ออกมา แล้วนำค่า
ออกมา แล้วนำค่า ![]() นั้นไปลงบนเส้นจำนวน จะพบว่า เส้นจำนวนถูกแบ่งเป็นช่วงสั้น ๆ
นั้นไปลงบนเส้นจำนวน จะพบว่า เส้นจำนวนถูกแบ่งเป็นช่วงสั้น ๆ
ขั้นที่ 3
ให้ขวามือสุดเป็นบวก จากนั้นใส่ – , + สลับไปเรื่อย ๆ
ขั้นที่ 4
ถ้าอสมการในขั้นที่ 1 เป็น ≥ 0 หรือ > 0 ให้ตอบช่วงที่เป็นบวก
แต่ถ้าเป็น ![]() หรือ
หรือ ![]() ให้ตอบช่วงที่เป็นลบ และสำหรับ
ให้ตอบช่วงที่เป็นลบ และสำหรับ ![]() (มีเครื่องหมาย = ร่วมด้วย) ให้ระบายจุด
(มีเครื่องหมาย = ร่วมด้วย) ให้ระบายจุด ![]() จากขั้นที่ 2 (จุดปลายของช่วง) เป็นคำตอบด้วย
จากขั้นที่ 2 (จุดปลายของช่วง) เป็นคำตอบด้วย


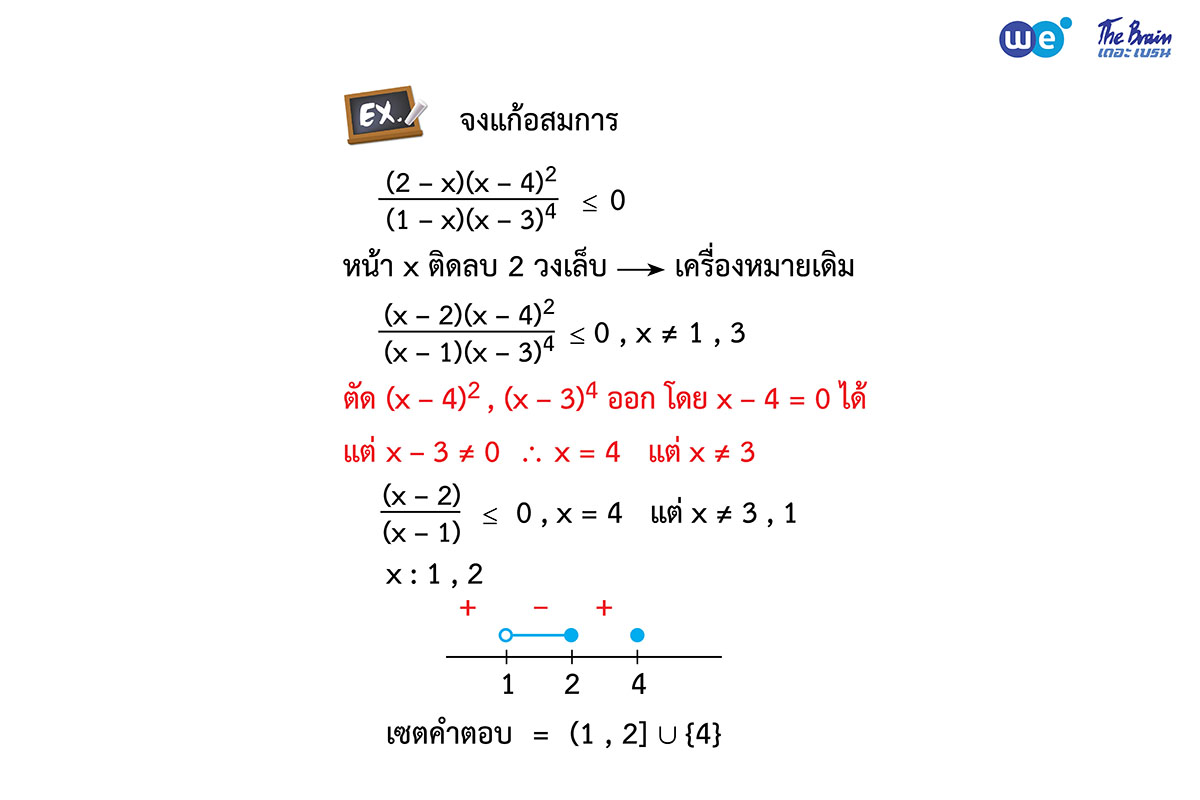
กรณีซ้ายมือมีวงเล็บด้านล่างด้วย ”วงเล็บหารกันทำเหมือนวงเล็บคูณกัน แต่เมื่อเป็นเศษส่วน ส่วนห้ามเป็นศูนย์“

ค่าสัมบูรณ์
นิยาม

สมบัติสำคัญ
1. ![]()
2. ![]()
3. ![]() สลับที่การลบได้ในค่าสัมบูรณ์
สลับที่การลบได้ในค่าสัมบูรณ์
4. ![]()
และ ![]() เมื่อ
เมื่อ ![]()
เช่น ![]()
และ ![]() เมื่อ
เมื่อ ![]()
5. ![]()
เช่น ![]()
6. ![]() เมื่อ
เมื่อ ![]() → เป็นจำนวนคี่บวก
→ เป็นจำนวนคี่บวก
![]() เมื่อ
เมื่อ ![]() → เป็นจำนวนคู่บวก
→ เป็นจำนวนคู่บวก
เช่น ![]()
แต่ ![]()
7. ![]()
![]()
ค่าสัมบูรณ์บวกกัน เสริมกัน ค่าจึงมาก
![]()
![]()
ค่าสัมบูรณ์ลบกัน หักล้าง ค่าจึงน้อย


8. ![]() เมื่อ
เมื่อ ![]()
![]() เมื่อ
เมื่อ ![]()


การแก้สมการที่ติดค่าสัมบูรณ์
การแก้สมการที่ติดค่าสัมบูรณ์ มีรูปแบบหลัก 4 รูปแบบ ได้แก่
1. |☐| = ตัวเลขบวก
หลักการ แยก 2 กรณี
“เท่ากับตัวเดิม หรือ เท่ากับตัวติดลบ”

2. |☐| = ∆
หลักการ แยก 2 กรณี และต้องตรวจคำตอบด้วย โดย ∆ ≥ 0
“เท่ากับตัวเดิม หรือ เท่ากับตัวติดลบ และ ตรวจคำตอบด้วย”

ตรวจคำตอบ ➝ ให้นำคำตอบไปแทนใน ![]() ถ้าออกมาเป็น บวกหรือเป็นศูนย์ คำตอบนั้นใช้ได้ ถ้าเป็นลบให้ตัดคำตอบนั้นทิ้ง
ถ้าออกมาเป็น บวกหรือเป็นศูนย์ คำตอบนั้นใช้ได้ ถ้าเป็นลบให้ตัดคำตอบนั้นทิ้ง
![]() ✗
✗
![]() ✓
✓
![]() ✓
✓
∴ เซตคำตอบ = ![]()
3. |☐| = ☐ อ้าง ☐ ≥ 0
|☐| = – ☐ อ้าง ☐ ≤ 0


4. |☐| = |∆|
หลักการ ยกกำลัง 2 ทั้งสองข้าง หรือใช้สูตร
☐ = ∆ หรือ ☐ = – ∆
“เท่ากับตัวเดิม หรือ เท่ากับตัวติดลบ”

สำหรับสมการที่ติดค่าสัมบูรณ์ที่นอกเหนือจาก 4 รูปแบบนี้ที่พี่ยกตัวอย่างมาให้ดูกัน จะใช้การแบ่งกรณี หรือสมบัติต่าง ๆ ช่วยแก้ครับ
การแก้อสมการที่ติดค่าสัมบูรณ์
การแก้อสมการที่ติดค่าสัมบูรณ์ มีรูปแบบหลัก 3 รูปแบบ ได้แก่
1. |☐| ≥ a
จะได้ ☐ ≥ a หรือ ☐ ≤ -a
|☐| > a
จะได้ ☐ > a หรือ ☐ < -a
“ค่าสัมบูรณ์ต่อด้วยเครื่องหมายมากกว่าจะได้มากกว่าตัวเดิม หรือ น้อยกว่าตัวติดลบ”
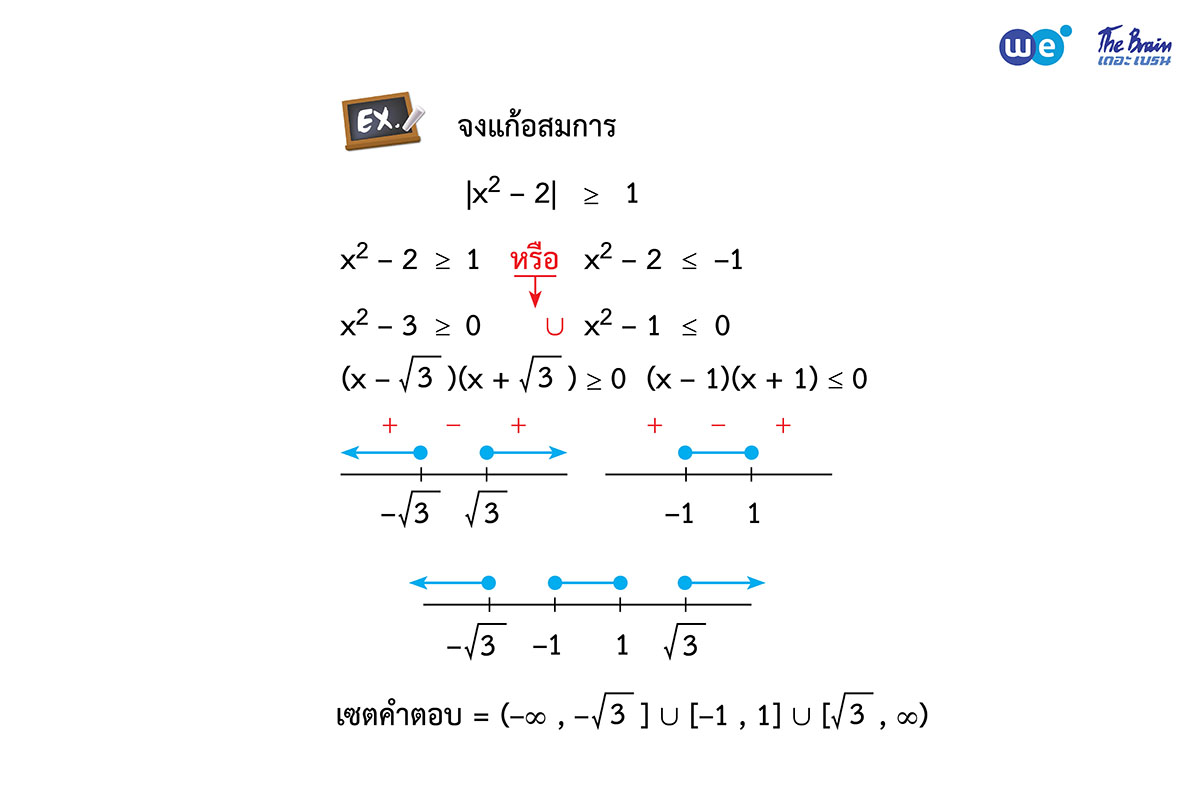
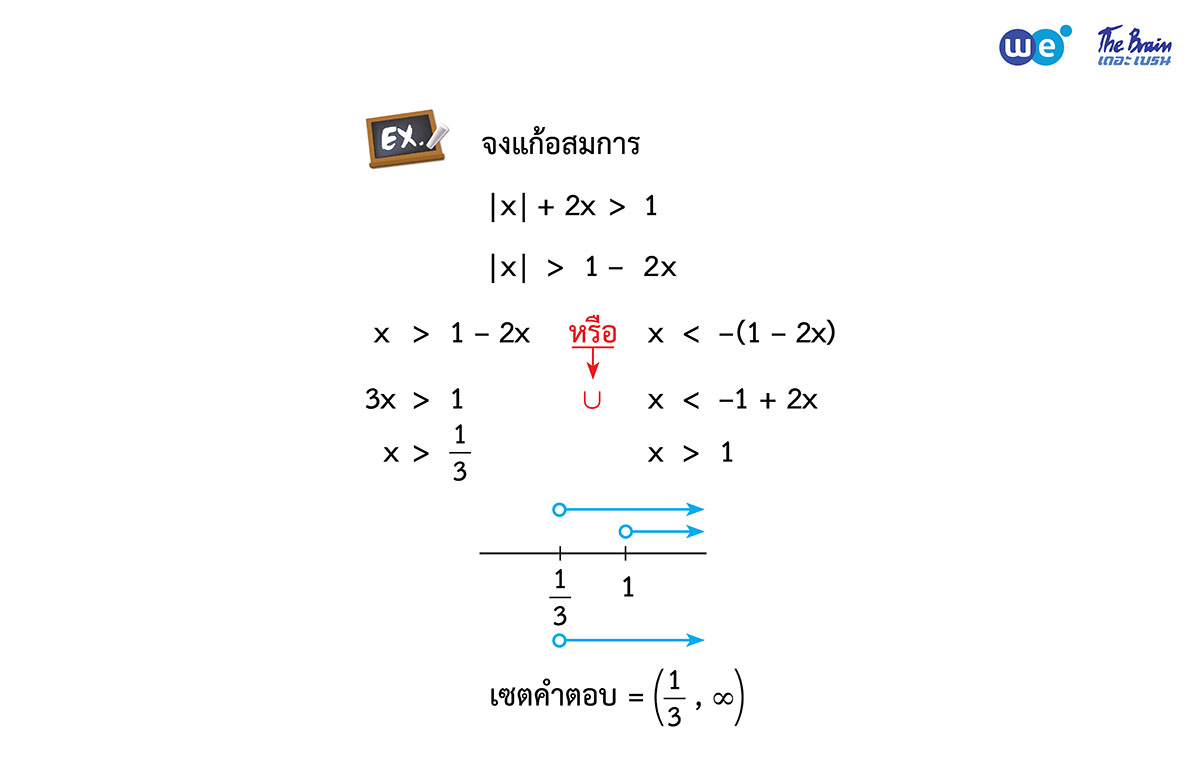
2. |☐| ≤ a
จะได้ -a ≤ ☐ ≤ a
|☐| < a
จะได้ -a < ☐ < a
“ค่าสัมบูรณ์ต่อด้วยเครื่องหมายน้อยกว่า จะได้อยู่ระหว่างตัวติดลบกับตัวเดิม”

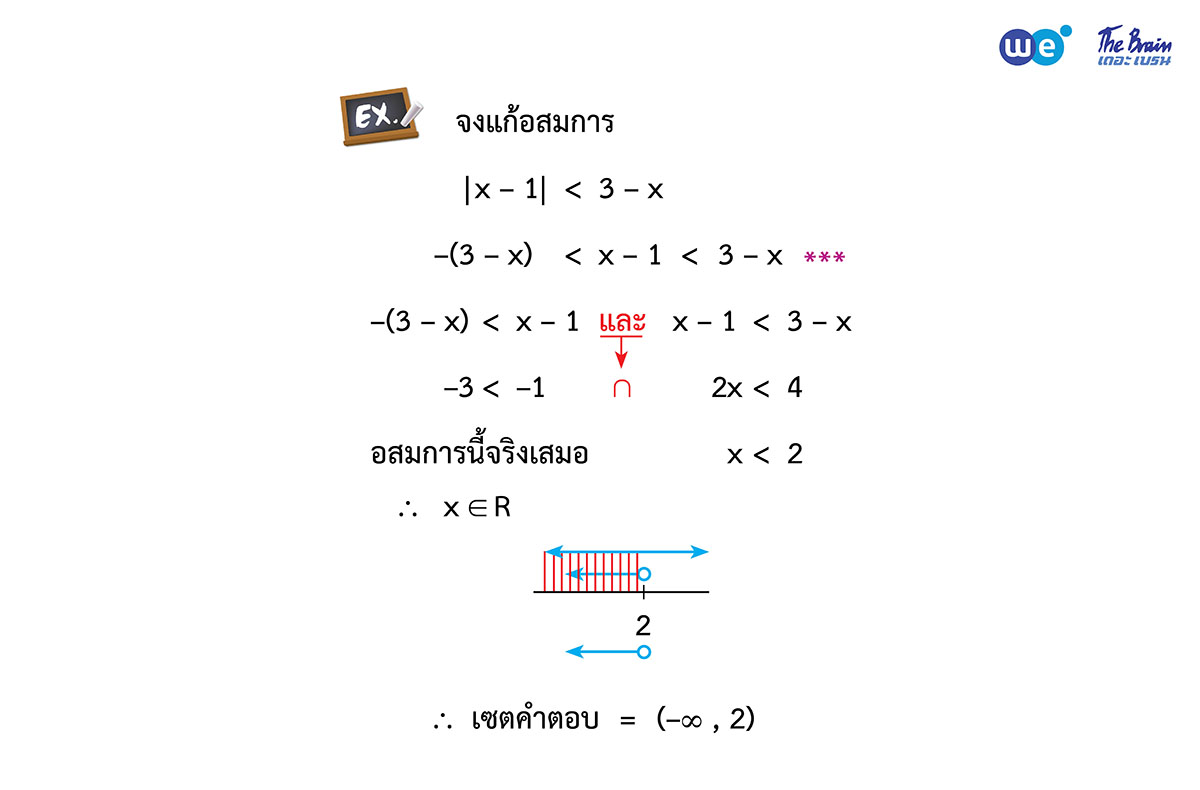
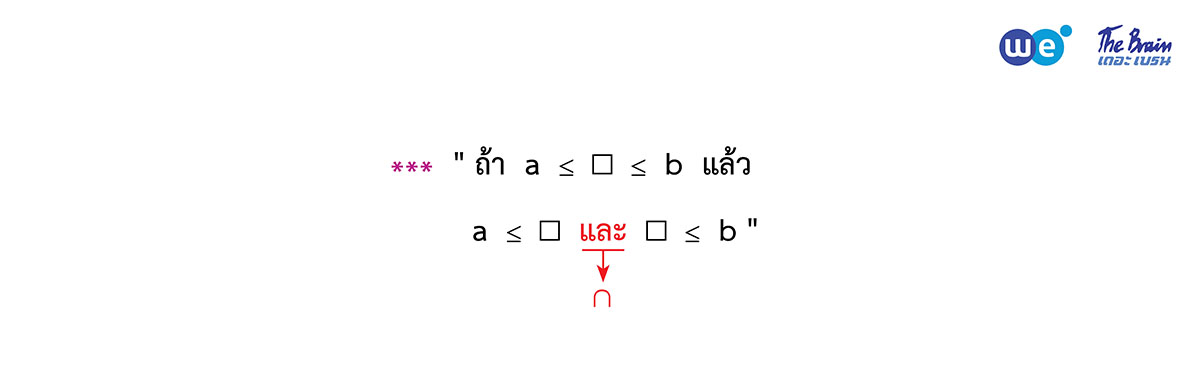
3. |☐| ≥ |∆| (หรือ > หรือ ≤ หรือ <)
หลักการ ยกกำลัง 2 ทั้งสองข้าง หรือใช้สูตร
(☐ – ∆)(☐ + ∆) ≥ 0
“หน้าลบหลัง คูณ หน้าบวกหลัง เครื่องหมายเดิม ตามด้วยศูนย์”

สำหรับอสมการที่ติดค่าสัมบูรณ์ที่นอกเหนือจาก 3 รูปแบบนี้ จะใช้การแบ่งกรณี หรือสมบัติต่าง ๆ ช่วยแก้ครับ
เทคนิคการแบ่งกรณี
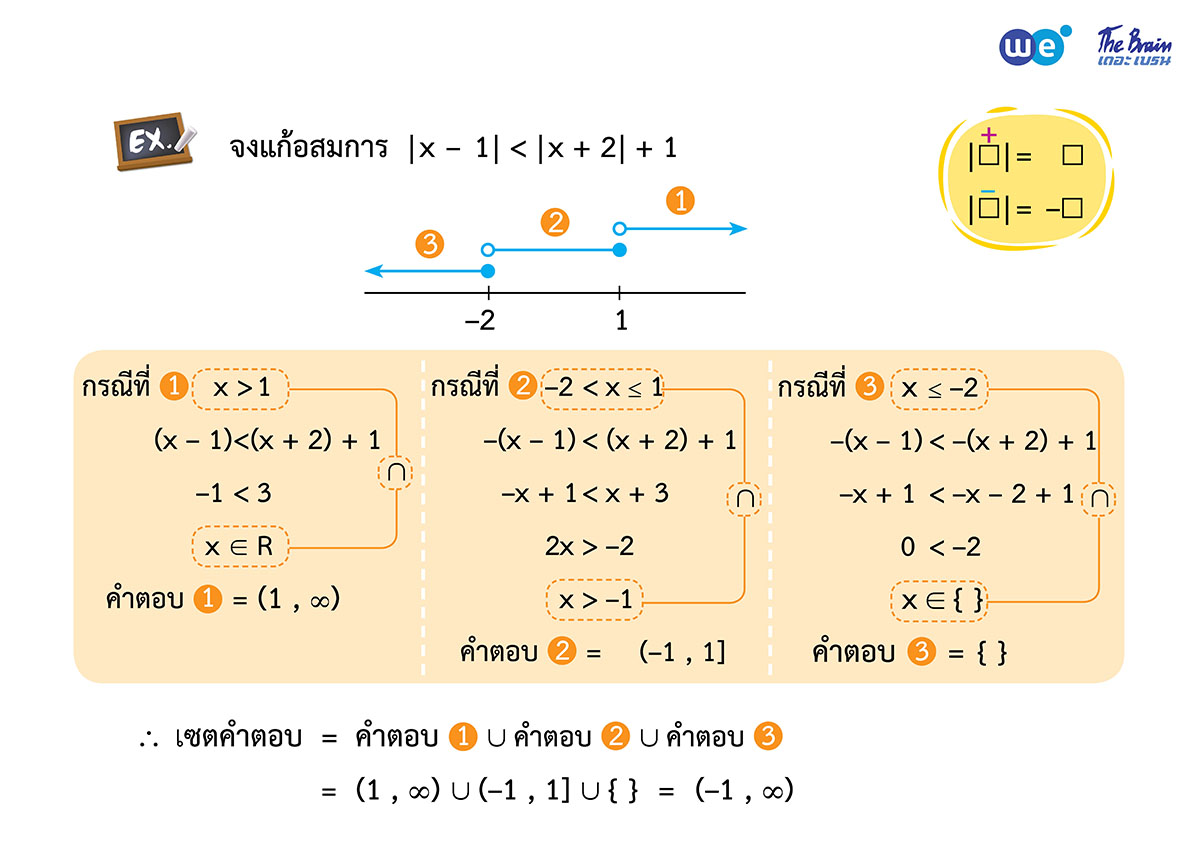
การแก้สมการและอสมการที่ติดรูท (√)
สมการติดรูท
หลักการ ยกกำลัง 2 และตรวจคำตอบเสมอ

อสมการติดรูท
หลักการ
ขั้นที่ 1 สร้างเงื่อนไข ![]() → ☐ ≥ 0
→ ☐ ≥ 0
ถ้ามีมากกว่า 1 เงื่อนไข ให้นำมา ∩ กัน
ขั้นที่ 2 ยกกำลัง 2 โดย 2 ข้างต้อง ≥ 0
ขั้นที่ 3 นำคำตอบ ∩ เงื่อนไข

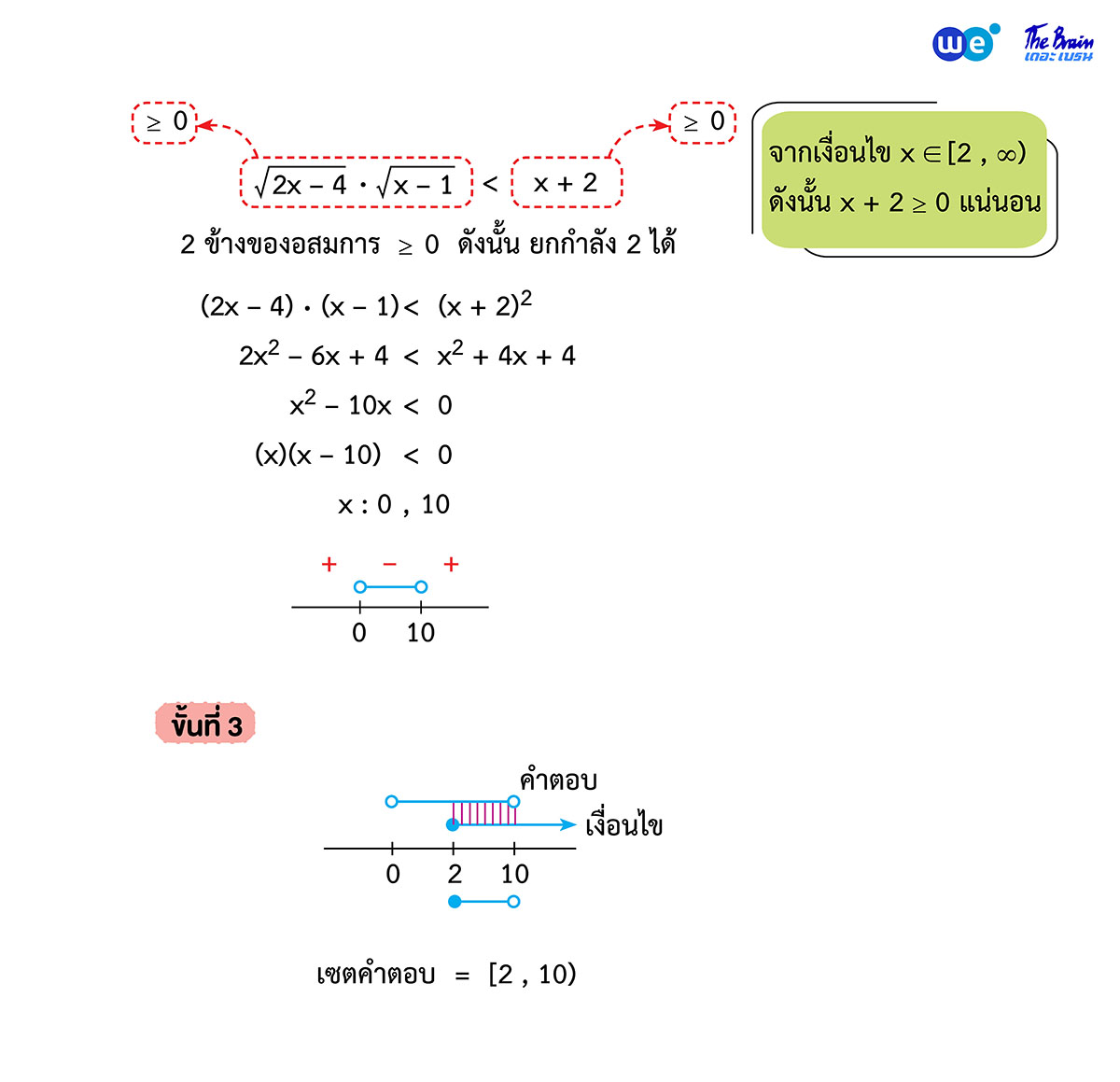
ตัวอย่างข้อสอบคณิตศาสตร์ พร้อมเฉลย - จำนวนจริง
หลังจากที่น้อง ๆ ได้ทบทวนเนื้อหาและสูตรสำคัญของบทจำนวนจริง ม.4 จบไปแล้ว คราวนี้มาลองแก้โจทย์คณิตศาสตร์บทนี้บ้างดีกว่า โดยพี่รวบรวม ตัวอย่างข้อสอบเข้ามหาวิทยาลัย วิชาคณิคศาสตร์ บทจำนวนจริง พร้อมเฉลยละเอียด มาฝากกัน ถ้าพร้อมแล้วก็ลุยได้เลย!!
โจทย์จำนวนจริง พร้อมเฉลย ข้อที่ 1

โจทย์จำนวนจริง พร้อมเฉลย ข้อที่ 2

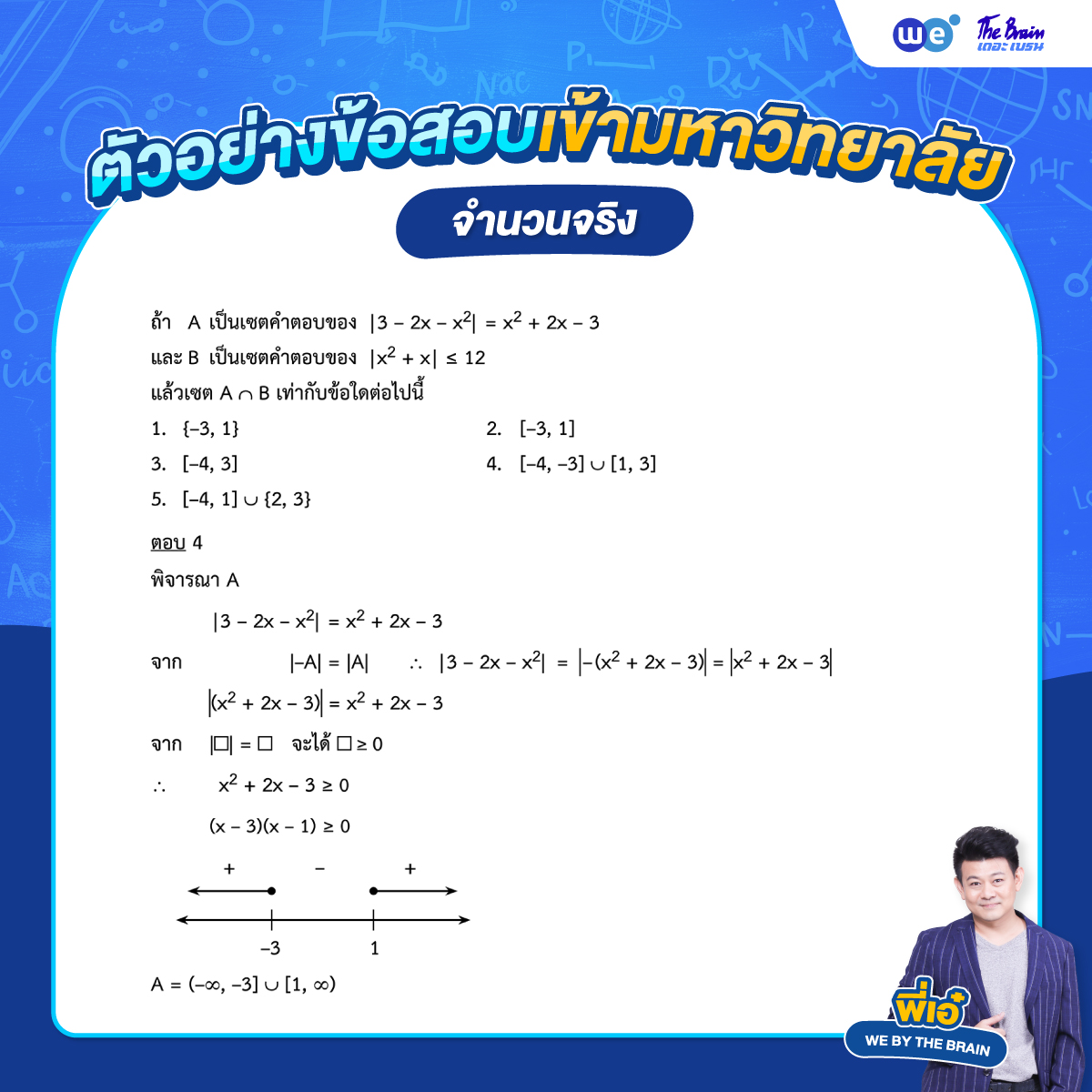
โจทย์จำนวนจริง พร้อมเฉลย ข้อที่ 3

โจทย์จำนวนจริง พร้อมเฉลย ข้อที่ 4

โจทย์จำนวนจริง พร้อมเฉลย ข้อที่ 5

ติวคณิตศาสตร์ ม.4 กับ WE BY THE BRAIN พร้อมพิชิตเกรด 4 และสนามสอบเข้ามหาวิทยาลัย
พี่เอ๋หวังว่าบทความนี้จะช่วยให้น้อง ๆ ได้รับความรู้และมีความเข้าใจในเนื้อหา บทจำนวนจริง ม.4 มากขึ้นนะครับ แล้วสำหรับใครที่อยากจะติวคณิตศาสตร์ ม.ปลาย บทนี้ให้พื้นฐานแน่นยิ่งขึ้น ก็สมัคร คอร์สคณิตศาสตร์ ม.4 เทอม 1 รวมทุกบท กับ “เดอะเบรน” ได้เลย!!
สมัครคอร์สนี้ดียังไง?
✔ เนื้อหาที่เรียนในคอร์สเรียนตรงตามหลักสูตรของ สสวท. ประกอบด้วยบทเซต ตรรกศาสตร์ และระบบจำนวนจริง
✔ สรุปเนื้อหาไว้แบบกระชับเข้าใจง่าย โดยพี่ ๆ ติวเตอร์ทีมคณิตศาสตร์จะช่วยปูพื้นฐานให้อย่างละเอียด
✔ พร้อมพาตะลุยโจทย์หลากหลาย ไล่ระดับตั้งแต่ง่าย – ยาก ที่เป็นข้อสอบแข่งขันจากสนามสอบต่าง ๆ ทั้งในและต่างประเทศ
✔ เสริมด้วยเทคนิคทริกลัดที่ช่วยให้แก้โจทย์ไว ใช้ได้จริงในห้องสอบ พร้อมพิชิตข้อสอบคณิตศาสตร์อย่างมั่นใจ
คอร์สนี้เหมาะกับใคร?
✔ คอร์สนี้เหมาะสำหรับน้อง ม.3 ที่กำลังจะขึ้น ม.4 ที่ต้องการเตรียมตัวล่วงหน้า
✔ คอร์สนี้เหมาะสำหรับน้อง ม.4 ที่ต้องการเรียนควบคู่ไปกับที่โรงเรียน เพื่อทำเกรดวิชาคณิตศาสตร์ และเป็นพื้นฐานสำคัญในการเตรียมตัวสอบเข้ามหาวิทยาลัย วิชาคณิตศาสตร์ประยุกต์1 A-Level ในระบบ TCAS
ใครอยากเก่งคณิต อยากได้โจทย์และเทคนิคดี ๆ จาก พี่ ๆ ติวเตอร์ ทีมคณิตศาสตร์ รีบกดติดตามก่อนใครได้ที่ช่องทางด้านล่างนี้เลย!
- Facebook Page : WE BY THE BRAIN
- Instagram : webythebrain
- Youtube : WE BY THE BRAIN
- Tiktok : คณิต เดอะเบรน
- Lemon8 : คณิต เดอะเบรน

อ.วิเศษ กี่สุขพันธ์ (พี่เอ๋)
ปริญญาตรี-โท วิศวกรรมศาสตร์ จุฬาลงกรณ์มหาวิทยาลัย
ประสบการณ์การสอน 24 ปี